题目内容
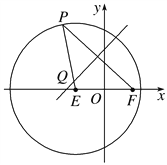
【题目】已知点![]() ,圆
,圆![]() 。
。
(1)若点![]() 在圆
在圆![]() 内,求
内,求![]() 的取值范围;
的取值范围;
(2)若过点![]() 的圆
的圆![]() 的切线只有一条,求切线的方程;
的切线只有一条,求切线的方程;
(3)当![]() 时,过点
时,过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程。
的方程。
【答案】(1)![]() ;(2)答案见解析;(3)x-y+2=0或7x+y-10=0。
;(2)答案见解析;(3)x-y+2=0或7x+y-10=0。
【解析】
(1)由题意求解不等式确定a的取值范围即可;
(2)首先确定a的值,然后求解切线方程即可;
(3)首先求得直线的斜率,然后求解直线方程即可.
(1)由题意可得:![]() ,求解不等式可得
,求解不等式可得![]() 的取值范围是
的取值范围是![]() ;
;
(2)由题意可知,点在圆上,故![]() ,
,
![]() 时,切线的斜率为
时,切线的斜率为![]() ,切线方程为
,切线方程为![]() ;
;
![]() 时,切线的斜率为
时,切线的斜率为![]() ,切线方程为
,切线方程为![]()
(3)设圆心到直线的距离为![]() ,由题意可得
,由题意可得![]() ,故
,故![]() ,
,
很明显直线的斜率存在,设直线方程为![]() ,即
,即![]() ,
,
由题意可得:![]() ,
,
解得:![]() 或
或![]()
方程为:x-y+2=0或7x+y-10=0。

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】为研究昼夜温差大小与某疾病的患病人数之间的关系,经查询得到今年上半年每月15号的昼夜温差情况与患者的人数如表:
日期 | 1月15日 | 2月15日 | 3月15日 | 4月15日 | 5月15日 | 6月15日 |
昼夜温差 | 10 | 11 | 10 | 10 | 9 | 7 |
患者人数 | 21 | 26 | 20 | 18 | 16 | 8 |
研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
![]() 若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程
若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程![]() ;
;
![]() 若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问
若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问![]() 中所得线性回归方程是否理想?
中所得线性回归方程是否理想?
参考公式:![]() ,
,![]()