题目内容
【题目】已知椭圆![]() (
(![]() )的上顶点与抛物线
)的上顶点与抛物线![]() (
(![]() )的焦点
)的焦点![]() 重合.
重合.
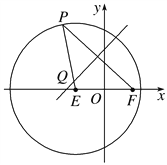
(1)设椭圆和抛物线交于![]() ,
, ![]() 两点,若
两点,若![]() ,求椭圆的方程;
,求椭圆的方程;
(2)设直线![]() 与抛物线和椭圆均相切,切点分别为
与抛物线和椭圆均相切,切点分别为![]() ,
, ![]() ,记
,记![]() 的面积为
的面积为![]() ,求证:
,求证: ![]() .
.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】试题分析:(1)根据椭圆几何性质得p,再根据对称性得A坐标,代人椭圆方程可得a,(2)先根据导数几何意义得抛物线切线方程,再与椭圆方程联立,根据判别式为零确定切点,根据三角形面积公式表示面积,最后根据基本不等式求最值,证得结论.
试题解析:(1)易知![]() ,则抛物线的方程为
,则抛物线的方程为![]()
由![]() 及图形的对称性,不妨设
及图形的对称性,不妨设![]() ,
,
代入![]() ,得
,得![]() ,则
,则![]() .
.
将之代入椭圆方程得 ,得
,得![]() ,
,
所以椭圆的方程为![]() .
.
(2)设切点![]() ,
, ![]() 即
即![]() ,求导得
,求导得![]() ,则切线
,则切线![]() 的斜率为
的斜率为![]() ,方程
,方程![]() ,即
,即![]() ,
,
将之与椭圆![]() 联立得
联立得![]() ,
,
令判别式![]()
化简整理得![]() ,
, ![]() ,此时
,此时![]()
设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,则
,则
![]()


由基本不等式得![]() ,
, ![]()
则 ,仅当
,仅当![]() 时取等号,但此时
时取等号,但此时![]() ,故等号无法取得,于是
,故等号无法取得,于是![]() .
.

【题目】由国家公安部提出,国家质量监督检验检疫总局发布的《车辆驾驶人员血液、呼气酒精含量阀值与检验标准(![]() )》于
)》于![]() 年
年![]() 月
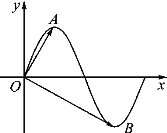
月![]() 日正式实施.车辆驾驶人员酒饮后或者醉酒后驾车血液中的酒精含量阀值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,
日正式实施.车辆驾驶人员酒饮后或者醉酒后驾车血液中的酒精含量阀值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,

喝![]() 瓶啤酒的情况
瓶啤酒的情况
且图表示的函数模型 ,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:
,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:![]() ,
,![]() )
)
( )
驾驶行为类型 | 阀值 |
饮酒后驾车 |
|
醉酒后驾车 |
|
车辆驾车人员血液酒精含量阀值
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
表1:甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 4 | 19 | 20 | 5 | 1 |
图1:乙套设备的样本的频率分布直方图

(1)填写下面列联表,并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关;
甲套设备 | 乙套设备 | 合计 | |||||||||||||
合格品 | |||||||||||||||
不合格品 | |||||||||||||||
合计 | ,求 |
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 .
.