题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(I)由离心率可得![]() 关系,再将点
关系,再将点![]() 坐标代入,可得
坐标代入,可得![]() 间关系,又
间关系,又![]() ,解方程可得
,解方程可得![]() 的值;(II)由
的值;(II)由![]() 的角平分线总垂直于
的角平分线总垂直于![]() 轴,可判断直线
轴,可判断直线![]() 的斜率互为相反数,由两直线都过
的斜率互为相反数,由两直线都过![]() 点,由点斜式可写出直线方程.一一与椭圆方程联立,消去
点,由点斜式可写出直线方程.一一与椭圆方程联立,消去![]() 的值,可得一元二次方程,又
的值,可得一元二次方程,又![]() 点满足条件,可求得
点满足条件,可求得![]() 点的坐标,用
点的坐标,用![]() 表示.再由斜率公式可得直线
表示.再由斜率公式可得直线![]() 的斜率为定值.
的斜率为定值.
试题解析:
(Ⅰ) 因为椭圆![]() 的离心率为
的离心率为![]() , 且过点
, 且过点![]() ,
,
所以![]() ,
, ![]() .
.
因为![]() ,
,
解得![]() ,
, ![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)法1:因为![]() 的角平分线总垂直于
的角平分线总垂直于![]() 轴, 所以
轴, 所以![]() 与
与![]() 所在直线关于直线
所在直线关于直线![]() 对
对
称. 设直线![]() 的斜率为
的斜率为![]() , 则直线
, 则直线![]() 的斜率为
的斜率为![]() .
.
所以直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
设点![]() ,
, ![]() ,
,
由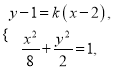 消去
消去![]() ,得
,得![]() . ①
. ①
因为点![]() 在椭圆
在椭圆![]() 上, 所以
上, 所以![]() 是方程①的一个根, 则
是方程①的一个根, 则![]() ,
,
所以![]() .
.
同理![]() .
.
所以![]() .
.
又![]() .
.
所以直线![]() 的斜率为
的斜率为![]() .
.
所以直线![]() 的斜率为定值,该值为
的斜率为定值,该值为![]() .
.
法2:设点![]() ,
,
则直线![]() 的斜率
的斜率![]() , 直线
, 直线![]() 的斜率
的斜率![]() .
.
因为![]() 的角平分线总垂直于
的角平分线总垂直于![]() 轴, 所以
轴, 所以![]() 与
与![]() 所在直线关于直线
所在直线关于直线![]() 对称.
对称.
所以![]() , 即
, 即![]() , ①
, ①
因为点![]() 在椭圆
在椭圆![]() 上,
上,
所以![]() ,②
,②
![]() . ③
. ③
由②得![]() , 得
, 得![]() , ④
, ④
同理由③得![]() , ⑤
, ⑤
由①④⑤得![]() ,
,
化简得![]() , ⑥
, ⑥
由①得![]() , ⑦
, ⑦
⑥![]() ⑦得
⑦得![]() .
.
②![]() ③得
③得![]() ,得
,得![]() .
.
所以直线![]() 的斜率为
的斜率为![]() 为定值.
为定值.
法3:设直线![]() 的方程为
的方程为![]() ,点
,点![]() ,
,
则![]() ,
,
直线![]() 的斜率
的斜率![]() , 直线
, 直线![]() 的斜率
的斜率![]() .
.
因为![]() 的角平分线总垂直于
的角平分线总垂直于![]() 轴, 所以
轴, 所以![]() 与
与![]() 所在直线关于直线
所在直线关于直线![]() 对称.
对称.
所以![]() , 即
, 即![]() ,
,
化简得![]() .
.
把![]() 代入上式, 并化简得
代入上式, 并化简得
![]() . (*)
. (*)
由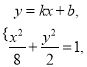 消去
消去![]() 得
得![]() , (**)
, (**)
则![]() ,
,
代入(*)得![]() ,
,
整理得![]() ,
,
所以![]() 或
或![]() .
.
若![]() , 可得方程(**)的一个根为
, 可得方程(**)的一个根为![]() ,不合题意.
,不合题意.
若![]() 时, 合题意.
时, 合题意.
所以直线![]() 的斜率为定值,该值为
的斜率为定值,该值为![]() .
.