题目内容
【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如下表:
x |
|
|
|
|
|
|
|
y | ﹣1 | 1 | 3 | 1 | ﹣1 | 1 | 3 |
(1)根据表格提供的数据求函数f(x)的一个解析式.
(2)根据(1)的结果,若函数y=f(kx)(k>0)周期为 ![]() ,当
,当 ![]() 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
【答案】
(1)解:设f(x)的最小正周期为T,得 ![]() ,
,
由 ![]() ,得ω=1,
,得ω=1,
又 ![]() ,解得
,解得 ![]()
令 ![]() ,即
,即 ![]() ,解得
,解得 ![]() ,
,
∴ ![]()
(2)解:∵函数 ![]() 的周期为
的周期为 ![]() ,
,
又k>0,∴k=3,
令 ![]() ,∵
,∵ ![]() ,∴
,∴ ![]() ,
,
如图,sint=s在 ![]() 上有两个不同的解,则
上有两个不同的解,则 ![]() ,
,
∴方程f(kx)=m在 ![]() 时恰好有两个不同的解,则
时恰好有两个不同的解,则 ![]() ,
,
即实数m的取值范围是 ![]() .
.
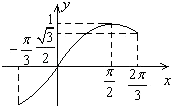
【解析】(1)根据表格提供的数据,求出周期T,解出ω,利用最小值、最大值求出A、B,结合周期求出φ,可求函数f(x)的一个解析式.(2)函数y=f(kx)(k>0)周期为 ![]() ,求出k,
,求出k, ![]() ,推出
,推出 ![]() 的范围,画出图象,数形结合容易求出m的范围.
的范围,画出图象,数形结合容易求出m的范围.

练习册系列答案
相关题目