Question

【题目】已知椭圆：的一个焦点与抛物线的焦点相同， ，为椭圆的左、右焦点．为椭圆上任意一点，△面积的最大值为1．

（1）求椭圆的方程；

（2）直线：交椭圆于，两点．

（i）若直线与的斜率分别为，，且，求证：直线过定点，并求出该定点的坐标；

（ii）若直线的斜率时直线，斜率的等比中项，求△面积的取值范围．

Answer 1

【答案】（1）（2）（i）（ii）

【解析】

试题分析：（1）先根据抛物线的焦点得，再结合椭圆几何条件得当点为椭圆的短轴端点时，△面积最大，此时，所以．（2）（i）证明直线过定点问题，一般方法以算代证，即求出直线方程，根据方程特征确定其过定点，本题关键求出之间关系即可得出直线过定点．由得，即，因此联立直线与椭圆方程，结合韦达定理可得；（ii）先分析条件：直线的斜率时直线，斜率的等比中项，即，，化简得，联立直线与椭圆方程，结合韦达定理可得，这样三角形面积可用m表示，其中高利用点到直线距离得到，底边边长利用弦长公式得到：，最后根据基本不等式求最值

试题解析：（1）由抛物线的方程得其焦点为，所以椭圆中，

当点为椭圆的短轴端点时，△面积最大，此时，所以．

，为椭圆的左、右焦点，为椭圆上任意一点，△面积的最大值为1，

所以椭圆的方程为．

（2）联立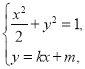得，

，得（*）

设，，则，，

（i），，由，得，

所以，即，

得，

所以直线的方程为，因此直线恒过定点，该定点坐标为．

（ii）因为直线的斜率是直线，斜率的等比中项，所以，即，

得，得，所以，又，所以，

代入（*），得．

．

设点到直线的距离为，则，

所以，

当且仅当，即时，△面积取最大值．

故△面积的取值范围为．