题目内容
13.求值域.(1)y=$\left\{\begin{array}{l}{x-2,x≥3}\\{-2x-1,x≤0}\end{array}\right.$.
(2)y=$\frac{2{x}^{2}+2x+3}{{x}^{2}+x+1}$.
分析 (1)根据分段函数的表达式进行求解即可.
(2)利用判别式△法进行求解即可.
解答 解:(1)当x≥3时,y=x-2≥3-2=1,
当x≤0时,y=-2x-1≥-1,
综上y≥-1,
即函数的值域为[1,+∞).
(2)∵x2+x+1>0恒成立,
∴函数的定义域为(-∞,+∞),
由y=$\frac{2{x}^{2}+2x+3}{{x}^{2}+x+1}$得(x2+x+1)y=2x2+2x+3,
即(2-y)x2+(2-y)x+3-y=0,
若y=2,在方程等价为3-2=0,即1=0,则方程不成立,
∴y≠2,
则由判别式△≥0得(2-y)2-4(2-y)(3-y)=(2-y)[2-y-4(3+y)]≥0,
即(y-2)(5y+10)≤0,
解得-2≤y≤2,
∵y≠2,
∴-2≤y<2,
即函数的值域为[-2,2).
点评 本题主要考查函数值域的求解,利用判别式法和函数的单调性法是解决本题的关键.

练习册系列答案
相关题目
1.函数y=$\frac{{x}^{2}+2x+6}{x-1}$(x>1)的最小值为( )
| A. | 10 | B. | 9 | C. | 6 | D. | 4 |
8.${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$(cos$\frac{x}{2}$-sin$\frac{x}{2}$)2dx=( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
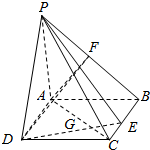 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AB=PA=1,AD=$\sqrt{3}$,E、F、G分别是BC、PB、AD上的点,且AF⊥PC,AG=3GD.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AB=PA=1,AD=$\sqrt{3}$,E、F、G分别是BC、PB、AD上的点,且AF⊥PC,AG=3GD. 如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,若BC=2,BD=6,则AB的长为2$\sqrt{3}$.
如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,若BC=2,BD=6,则AB的长为2$\sqrt{3}$.