题目内容
9.已知函数f(x)=ax-2lnx,a∈R(Ⅰ)当a=3时,求函数在(1,f(1))的切线方程
(Ⅱ)求函数f(x)的极值.
分析 (Ⅰ)把a=3代入函数解析式并求出导数,求出f′(1)和f(1),代入点斜式方程化简即可得到切线方程;
(Ⅱ)求出原函数的导函数和定义域,分a≤0和a>0讨论,分别由导函数的符号判断出函数单调区间,并求出函数的极值.
解答 解:(I)当a=3时,f(x)=3x-2lnx,则$f′(x)=3-\frac{2}{x}$,
∴f′(1)=3-2=1,且f(1)=3,
∴在(1,3)处的切线方程是:y-3=x-1,即x-y+2=0,…(4分)
(Ⅱ)由题意得,$f′(x)=a-\frac{2}{x}=\frac{ax-2}{x},x>0$,
当a≤0时,f′(x)<0,函数f(x)在(0,+∞)内是减函数,
∴函数f(x)没有极值. …(6分)
当a>0时,令f′(x)=0,得$x=\frac{2}{a}$,
当x变化时,f′(x)与f(x)变化情况如下表:
| x | $({0,\frac{2}{a}})$ | $\frac{2}{a}$ | $({\frac{2}{a},+∞})$ |
| f'(x) | - | 0 | + |
| f(x) | 单调递减 | 极小值 | 单调递增 |
综上,当a≤0时,f(x)没有极值;
当a>0时,f(x)的极小值为$2-2ln\frac{2}{a}$,没有极大值. …(9分)
点评 本题考查导数的几何意义以及切线方程,导数与函数的单调性、极值的关系,考查了分类讨论的数学思想方法,是中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
14.若复数z满足(z-3)(2-i)=5(i为虚数单位),则z为( )
| A. | 2-i | B. | 2+i | C. | 5-i | D. | 5+i |
1.为调差学生的身体素质情况,某教育局从当地各学校随机抽调50名学生,进行五项体能达标考核,并对每个学生考核成绩进行统计,请你根据尚未完成的频率分布表,解答下列问题:
(1)求表中a、b、c、d、e的值;
(2)作出频率分布直方图,并估算成绩的中位数.
| 分组 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 | 合计 |
| 频数 | 1 | b | 18 | c | 4 | 50 |
| 频率 | a | 0.24 | 0.36 | d | e | 1 |
(2)作出频率分布直方图,并估算成绩的中位数.
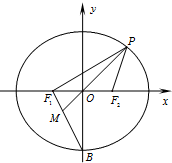 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{5}}{5}$,短轴长为4,F1、F2为椭圆左、右焦点,点B为下顶点.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{5}}{5}$,短轴长为4,F1、F2为椭圆左、右焦点,点B为下顶点.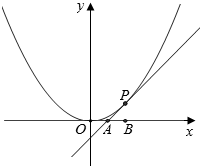 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).