Question

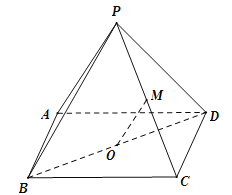
【题目】（本小题满分为14分）如图1所示，在Rt△ABC中，AC＝6，BC＝3，∠ABC＝90°，CD为∠ACB的平分线，点E在线段AC上，CE＝4.如图2所示，将△BCD沿CD折起，使得平面BCD⊥平面ACD，连结AB，设点F是AB的中点．

（1）求证：DE⊥平面BCD；

（2）在图2中，若EF∥平面BDG，其中G为直线AC与平面BDG的交点，求三棱锥BDEG的体积．

Answer 1

【答案】（1）详见解析（2）

【解析】

试题分析：（1）折叠问题需注意折叠前后垂直关系不变的量：折叠前根据平几知识可计算出有DE⊥CD.折叠后仍有DE⊥CD.再由面面垂直性质定理可得DE⊥平面BCD.（2）求三棱锥体积关键在于确定高，即线面垂直.这仍可由面面垂直性质定理得到：因为平面BCD⊥平面ACD，过点B作BH⊥CD交于点H 则有BH⊥平面ACD.由线面平行可推导出线线平行，从而确定G的位置，这样就可计算底面积，最后根据三棱锥体积公式求体积

试题解析：（1）证明：在题图1中，因为AC＝6，BC＝3，∠ABC＝90°，

所以∠ACB＝60°.

因为CD为∠ACB的平分线，所以∠BCD＝∠ACD＝30°，

所以CD＝2.

又因为CE＝4，∠DCE＝30°，所以DE＝2.则CD2＋DE2＝CE2，

所以∠CDE＝90°，即DE⊥CD.

在题图2中，因为平面BCD⊥平面ACD，平面BCD∩平面ACD＝CD，DE平面ACD，所以DE⊥平面BCD.

（2）在题图2中，因为EF∥平面BDG，EF平面ABC，

平面ABC∩平面BDG＝BG，所以EF∥BG.

因为点E在线段AC上，CE＝4，点F是AB的中点，

所以AE＝EG＝CG＝2.

过点B作BH⊥CD交于点H.因为平面BCD⊥平面ACD，BH平面BCD，

所以BH⊥平面ACD.

由条件得BH＝.又S△DEG＝S△ACD＝×AC·CD·sin 30°＝，

所以三棱锥BDEG的体积为V＝S△DEG·BH＝××＝.