题目内容
【题目】设双曲线 
=1（a＞0，b＞0）的右焦点为F，右顶点为A，过F作AF的垂线与双曲线的两条渐近线交于B、C两点，过B、C分别作AC、AB的垂线，两垂线交于点D．若D到直线BC的距离小于2（a+ 
），则该双曲线的离心率的取值范围是（ ）
A.（1，2）
B.（ 
，2）
C.（1， 
）
D.（ ， ）
【答案】C
【解析】解：由题意可得D为△ABC的垂心，
即有AD⊥BC，即D在x轴上，
令x=c，可得y2=b2（ 
﹣1），
解得y=± 
，
可设B（c， ），C（c，﹣ ），
由BD⊥AC，可得kBDkAC=﹣1，
由题意，A（a，0），
设D（x，0），则由BD⊥AB得 
=﹣1，
∴c﹣x= 
，
∵D到直线BC的距离小于2（a+ 
）=2（a+c），
∴c﹣x=| |＜2（a+c），
∴ 
＜2（c2﹣a2）=2b2 ，
∴（ 
）2＜2，
则b2＜2a2 ，
即c2﹣a2＜2a2 ，
则c2＜3a2 ，
c＜ 
a，
即1＜e＜ ，
则曲线的离心率的取值范围是（1， ），
故选：C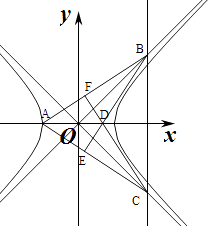
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
