题目内容
【题目】已知数列{an}的前n项和为Sn ， 且满足an+2SnSn﹣1=0（n≥2），a1= 
．
（1）求证：{ 
}是等差数列；
（2）求an的表达式．
【答案】
（1）证明：∵﹣an=2SnSn﹣1，
∴﹣Sn+Sn﹣1=2SnSn﹣1（n≥2），Sn≠0（n=1，2，3）．
∴ 
﹣ 
=2．
又 
= 
=2，∴{ }是以2为首项，2为公差的等差数列
（2）解：由（1）， =2+（n﹣1）2=2n，∴Sn= 
．
当n≥2时，an=Sn﹣Sn﹣1= ﹣ 
=﹣ 
〔或n≥2时，an=﹣2SnSn﹣1=﹣ 〕；
当n=1时，S1=a1= 
．
∴an=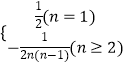 
【解析】（1）本题关键是将an=Sn﹣Sn﹣1代入化简，再根据等差数列的定义进行判定即可．（2）先求出Sn ， 利用Sn求an ， 必须分类讨论an= 
，求解可得．
【考点精析】利用等差关系的确定和数列的通项公式对题目进行判断即可得到答案，需要熟知如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，即
－
=d ，（n≥2，n∈N
）那么这个数列就叫做等差数列；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
练习册系列答案
相关题目
【题目】某公司过去五个月的广告费支出x与销售额y（单位：万元）之间有下列对应数据：
x | 2 | 4 | 5 | 6 | 8 |
y |
| 40 | 60 | 50 | 70 |
工作人员不慎将表格中y的第一个数据丢失．已知y对x呈线性相关关系，且回归方程为 
=6.5x+17.5，则下列说法：
①销售额y与广告费支出x正相关；
②丢失的数据（表中 
处）为30；
③该公司广告费支出每增加1万元，销售额一定增加6.5万元；
④若该公司下月广告投入8万元，则销售额为70万元．
其中，正确说法有（ ）
A.1个
B.2个
C.3个
D.4个
