题目内容
【题目】某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如表频率分布表:
分组 | 频数 | 频率 |
[39.95,39.97) | 6 | P1 |
[39.97,39.99) | 12 | 0.20 |
[39.99,40.01) | a | 0.50 |
[40.01,40.03) | b | P2 |
合计 | n | 1.00 |
(1)求a、b、n及P1、P2的值,并画出频率分布直方图(结果保留两位小数); 
(2)已知标准乒乓球的直径为40.00mm,直径误差不超过0.01mm的为五星乒乓球,若这批乒乓球共有10000个,试估计其中五星乒乓球的数目;
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间[39.99,40.01)的中点值是40.00)作为代表,估计这批乒乓球直径的平均值和中位数.
【答案】
(1)解:由频率分布表可知:
n=12÷0.20=60,
a=60×0.50=30,
b=60﹣6﹣12﹣30=12,
频率P1=6÷60=0.10,
频率P2=12÷60=0.20,
所以频率分布直方图如图所示:
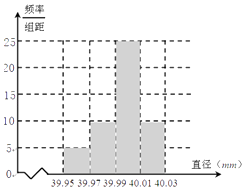
(2)解:五星乒乓球的直径落在[39.99,40.01]内,频率为
25×(40.01﹣39.99)=0.50;
故10000个乒乓球中“五星乒乓球”大约有:
10000×0.50=5000个
(3)解:平均数为
![]() ,
,
设中位数为m,则
39.99<m<40.01且0.10+0.20+(m﹣39.99)×25=0.50,
所以m=39.998,
即中位数为39.998
【解析】(1)由频率分布表,求出样本容量n,再计算a、b与频率P1、P2 ,
画出频率分布直方图;(2)求出直径落在[39.99,40.01]内的频率,计算对应的频数即可;(3)利用频率分布直方图计算平均数与中位数即可.
【考点精析】根据题目的已知条件,利用频率分布直方图和平均数、中位数、众数的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
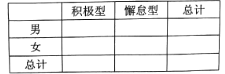
暑假接力赛新疆青少年出版社系列答案【题目】【2017重庆二诊】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
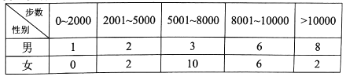
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附: 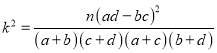 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【题目】某公司过去五个月的广告费支出x与销售额y(单位:万元)之间有下列对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y |
| 40 | 60 | 50 | 70 |
工作人员不慎将表格中y的第一个数据丢失.已知y对x呈线性相关关系,且回归方程为 ![]() =6.5x+17.5,则下列说法:
=6.5x+17.5,则下列说法:
①销售额y与广告费支出x正相关;
②丢失的数据(表中 ![]() 处)为30;
处)为30;
③该公司广告费支出每增加1万元,销售额一定增加6.5万元;
④若该公司下月广告投入8万元,则销售额为70万元.
其中,正确说法有( )
A.1个
B.2个
C.3个
D.4个