题目内容
13.设f(α)=$\frac{sin(π-α)cos(2π-α)}{cos(-α-π)tan(π+α)}$ 其中α是第三象限角.(1)化简f(α);
(2)若cos{$α-\frac{3π}{2}$)=$\frac{1}{5}$,求f(α);
(3)若α=-1860°,求f(α).
分析 (1)根据三角函数的诱导公式,结合同角三角函数的关系,化简f(α)即可;
(2)化简cos($α-\frac{3π}{2}$)=$\frac{1}{5}$,求出sinα、cosα的值,即可计算f(α)的值;
(3)利用诱导公式计算f(α)的值即可.
解答 解:(1)f(α)=$\frac{sin(π-α)cos(2π-α)}{cos(-α-π)tan(π+α)}$
=$\frac{sinαcosα}{cos(π+α)tanα}$
=$\frac{sinαcosα}{-cosα•\frac{sinα}{cosα}}$
=-cosα,(α是第三象限角);
(2)∵cos($α-\frac{3π}{2}$)=$\frac{1}{5}$,
∴cos($\frac{3π}{2}$-α)=$\frac{1}{5}$,
∴-sinα=$\frac{1}{5}$,
即sinα=-$\frac{1}{5}$;
∴cosα=-$\sqrt{1{-sin}^{2}α}$
=-$\sqrt{1{-(-\frac{1}{5})}^{2}}$
=-$\frac{2\sqrt{6}}{5}$,
∴f(α)=-cosα=$\frac{2\sqrt{6}}{5}$;
(3)∴α=-1860°,
∴f(α)=-cos(-1860°)
=-cos1860°
=-cos(60°+5×360°)
=-cos60°
=-$\frac{1}{2}$.
点评 本题考查了三角函数的计算与求值问题,考查了诱导公式的应用以及同角三角函数的关系应用问题,是基础题目.

练习册系列答案
相关题目
18.f(x)=ax2+bx+c满足f(0)=3,对称轴是直线x=-1,最小值为2,则该函数的表达式为( )
| A. | f(x)=x2-2x-3 | B. | f(x)=x2+2x-3 | C. | f(x)=x2-2x+3 | D. | f(x)=x2+2x+3 |
2.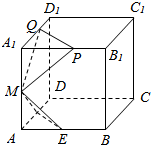 如图:已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1、A1D1上,且A1P=A1Q=x,0<x<1,设平面MEF∩平面MPQ=l,则下列结论中不成立的是( )
如图:已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1、A1D1上,且A1P=A1Q=x,0<x<1,设平面MEF∩平面MPQ=l,则下列结论中不成立的是( )
 如图:已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1、A1D1上,且A1P=A1Q=x,0<x<1,设平面MEF∩平面MPQ=l,则下列结论中不成立的是( )
如图:已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1、A1D1上,且A1P=A1Q=x,0<x<1,设平面MEF∩平面MPQ=l,则下列结论中不成立的是( )| A. | l∥平面ABCD | B. | 平面MEF与平面MPQ不垂直 | ||
| C. | l⊥BC1 | D. | 当x变化时,l是定直线 |
 一个几何体的三视图如图所示:
一个几何体的三视图如图所示: