题目内容
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.
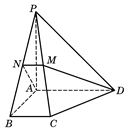
(Ⅰ)求证:PB⊥DM;
(Ⅱ)求CD与平面ADMN所成的角

(Ⅰ)求证:PB⊥DM;
(Ⅱ)求CD与平面ADMN所成的角
(I)见解析.(II)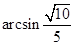 .
.
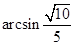 .
.本题主要考查空间线线、线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力.
(I)欲证PB⊥DM,可先证PB⊥平面ADMN,根据直线与平面垂直的判定定理可知只需证PB与平面ADMN内两相交直线垂直,而AN⊥PB,AD⊥PB,满足定理条件;
(II)取AD的中点G,连接BG、NG,得到 BG∥CD,从而BG与平面ADMN所成的角和CD与平面ADMN所成的角相等,根据线面所成角的定义可知∠BGN是BG与平面ADMN所成的角,在Rt△BGN中求出此角的正弦值即可.
解:(I)因为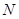 是
是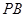 的中点,
的中点,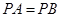 ,所以
,所以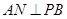 .
.
因为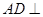 平面
平面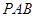 ,所以
,所以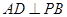 ,从而
,从而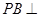 平面
平面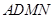 .
.
因为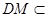 平面
平面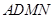 ,所以
,所以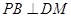 .
.
(II)取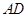 的中点
的中点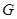 ,连结
,连结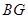 、
、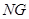 ,则
,则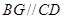 ,
,
所以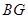 与平面
与平面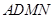 所成的角和
所成的角和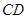 与平面
与平面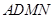 所成的角相等.
所成的角相等.
因为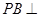 平面
平面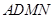 ,所以
,所以 是
是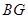 与平面
与平面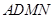 所成的角.
所成的角.
在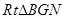 中,
中,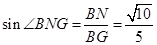 .
.
故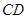 与平面
与平面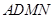 所成的角是
所成的角是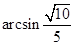 .
.
(I)欲证PB⊥DM,可先证PB⊥平面ADMN,根据直线与平面垂直的判定定理可知只需证PB与平面ADMN内两相交直线垂直,而AN⊥PB,AD⊥PB,满足定理条件;
(II)取AD的中点G,连接BG、NG,得到 BG∥CD,从而BG与平面ADMN所成的角和CD与平面ADMN所成的角相等,根据线面所成角的定义可知∠BGN是BG与平面ADMN所成的角,在Rt△BGN中求出此角的正弦值即可.
解:(I)因为
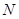 是
是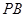 的中点,
的中点,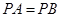 ,所以
,所以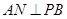 .
.因为
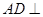 平面
平面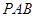 ,所以
,所以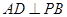 ,从而
,从而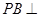 平面
平面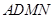 .
.因为
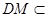 平面
平面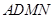 ,所以
,所以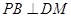 .
.(II)取
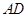 的中点
的中点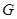 ,连结
,连结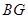 、
、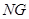 ,则
,则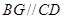 ,
,所以
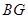 与平面
与平面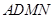 所成的角和
所成的角和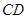 与平面
与平面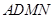 所成的角相等.
所成的角相等.因为
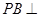 平面
平面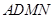 ,所以
,所以 是
是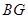 与平面
与平面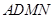 所成的角.
所成的角.在
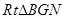 中,
中,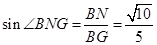 .
.故
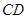 与平面
与平面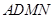 所成的角是
所成的角是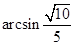 .
.
练习册系列答案
相关题目
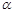 ∩平面
∩平面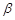 =AB,PQ⊥
=AB,PQ⊥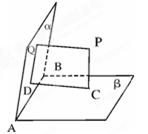
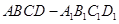 中,侧面
中,侧面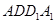 ⊥底面
⊥底面 ,
, ,底面
,底面
 ,O为
,O为 中点.
中点.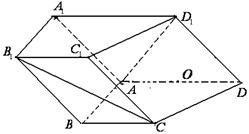
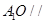 平面
平面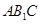 ;
;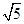 ,点M是PD的中点.
,点M是PD的中点.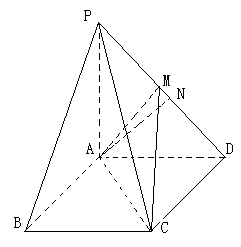
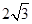 的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=400 ,
的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=400 ,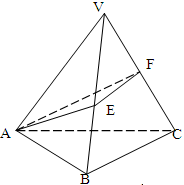
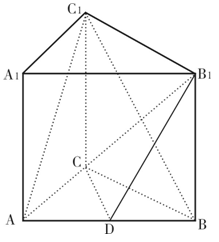
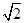 ,∠ACB=900,M是AA1的中点,N是BC1的中点.
,∠ACB=900,M是AA1的中点,N是BC1的中点.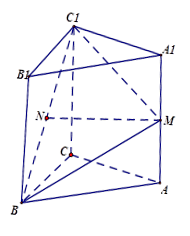
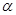 和直线l,则
和直线l,则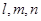 为三条不同的直线,
为三条不同的直线,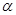 为一个平面,下列命题中正确的个数是 ( )
为一个平面,下列命题中正确的个数是 ( )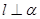 ,则
,则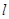 与
与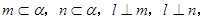 则
则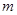 ,
, ,
,
 ,
,