题目内容
(本小题满分9分)
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.
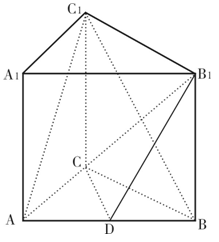
(1)求证AC⊥BC1
(2)求证AC1∥平面CDB1
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.

(1)求证AC⊥BC1
(2)求证AC1∥平面CDB1
见解析。
(1)通过证明AC⊥平面BCC1B1即可.
(2)证明DE//AC1即可.
证明:(1)∴CC1⊥底面ABC
∴CC1⊥AC……………………………………1分
∴AC=3 BC=4 AB=5
∴AC2+BC2=AB2
∴AC⊥BC……………………………………2分
∴AC⊥平面BCC1B1…………………………3分
∴AC⊥BC1……………………………………4分
(2)设BC1∩B1C=E连接DE
∵BCC1B1是矩形 ∴E是BC1的中点…………5分
又D是AB的中点,在△ABC1中,DE∥AC1……6分
又AC1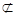 平面CDB1, DE
平面CDB1, DE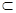 平面CDB1
平面CDB1
∴AC1∥平面CDB1……………………………8分
(2)证明DE//AC1即可.
证明:(1)∴CC1⊥底面ABC
∴CC1⊥AC……………………………………1分
∴AC=3 BC=4 AB=5
∴AC2+BC2=AB2
∴AC⊥BC……………………………………2分
∴AC⊥平面BCC1B1…………………………3分
∴AC⊥BC1……………………………………4分
(2)设BC1∩B1C=E连接DE
∵BCC1B1是矩形 ∴E是BC1的中点…………5分
又D是AB的中点,在△ABC1中,DE∥AC1……6分
又AC1
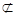 平面CDB1, DE
平面CDB1, DE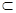 平面CDB1
平面CDB1∴AC1∥平面CDB1……………………………8分

练习册系列答案
相关题目
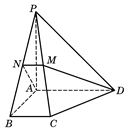
 中
中
 与
与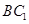 所成角的大小.
所成角的大小. 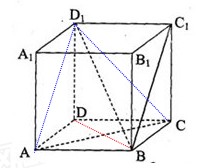
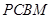 是直角梯形,
是直角梯形,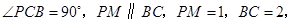 又
又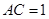 ,
,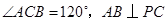 ,直线
,直线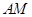 与直线
与直线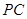 所成的角为
所成的角为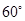 .
.
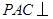 平面
平面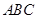 ;
;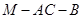 的大小;
的大小;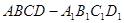 中,
中, 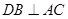 ,点
,点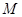 是棱
是棱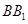 上一点.
上一点.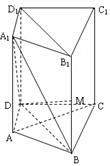
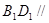 面
面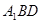 ;
;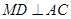 ;
;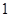
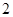
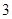
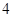
 与平面
与平面 平行的是( )
平行的是( )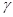
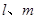 是
是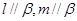
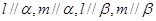

 、
、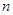 ,平面
,平面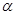 、
、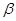 ,给出下列命题:
,给出下列命题: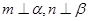 ,且
,且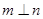 ,则
,则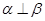 ②若
②若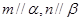 ,且
,且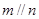 ,则
,则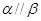
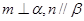 ,且
,且