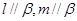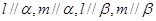题目内容
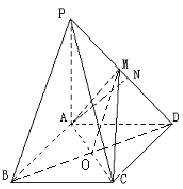
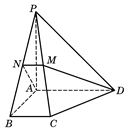
(本题满分12分)如图,底面为菱形的四棱锥P-ABCD中,∠ABC=60°,AC="1," PA="2," PB=PD=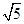 ,点M是PD的中点.
,点M是PD的中点.
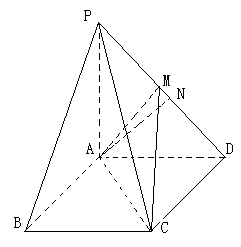
(Ⅰ)证明:PA⊥平面ABCD;
(Ⅱ)若AN为PD边的高线,求二面角M-AC-N的余弦值.
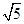 ,点M是PD的中点.
,点M是PD的中点.
(Ⅰ)证明:PA⊥平面ABCD;
(Ⅱ)若AN为PD边的高线,求二面角M-AC-N的余弦值.
证明:见解析;
(Ⅱ)
 .
.本试题主要是考查了线面垂直的判定和二面角平面角的求解的综合运用。
(1)要证明线面垂直,要通过判定定理线线垂直得到线面垂直,关键是证明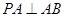 ,
, 。
。
(2)建立空间直角坐标系,然后表示出平面的法向量与法向量的夹角,进而求解二面角的平面角的大小的求解。
证明:(Ⅰ)∵菱形ABCD中∠ABC=60°,
∴ ABC为等边三角形
ABC为等边三角形
∴ --------1分
--------1分
又∵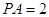 ,
,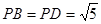
∴有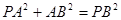 ,
,
∴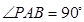 ,
,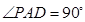 -------3分
-------3分
∴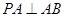 ,
, ,而
,而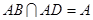
∴ 平面
平面 (4分)
(4分)
(Ⅱ)取BC中点E,连结AE,则AE⊥BC.以点A为坐标原点,AE为x轴正向,AD为y轴正向,AP为z轴正向建立空间直角坐标系,则
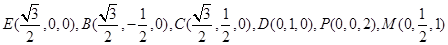 (5分)
(5分)
在 PAD内,AD="1," AP=2,∴PD=
PAD内,AD="1," AP=2,∴PD=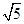 , AN=
, AN=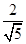 ,点
,点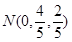
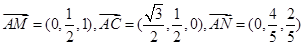 (6分)
(6分)
设平面AMC的一个法向量为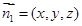 ,则
,则
 ,
,
令y="1," 则 ,得平面AMC的一个法向量
,得平面AMC的一个法向量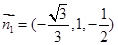 ;(8分)
;(8分)
设平面ANC的法向量为 ,则
,则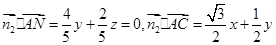 ,
,
令y="1," 得平面ANC的一个法向量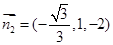 (10分)
(10分)
设二面角M-AC-N的平面角为 ,由图像知其必为锐角,从而有(12分)
,由图像知其必为锐角,从而有(12分)
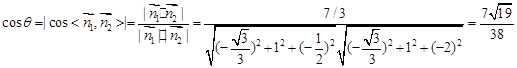 .
.
(1)要证明线面垂直,要通过判定定理线线垂直得到线面垂直,关键是证明
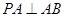 ,
, 。
。(2)建立空间直角坐标系,然后表示出平面的法向量与法向量的夹角,进而求解二面角的平面角的大小的求解。

证明:(Ⅰ)∵菱形ABCD中∠ABC=60°,
∴
 ABC为等边三角形
ABC为等边三角形∴
 --------1分
--------1分又∵
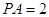 ,
,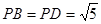
∴有
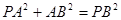 ,
,
∴
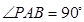 ,
,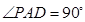 -------3分
-------3分∴
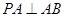 ,
, ,而
,而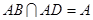
∴
 平面
平面 (4分)
(4分)(Ⅱ)取BC中点E,连结AE,则AE⊥BC.以点A为坐标原点,AE为x轴正向,AD为y轴正向,AP为z轴正向建立空间直角坐标系,则
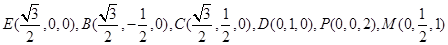 (5分)
(5分)在
 PAD内,AD="1," AP=2,∴PD=
PAD内,AD="1," AP=2,∴PD=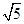 , AN=
, AN=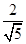 ,点
,点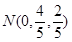
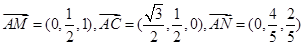 (6分)
(6分)设平面AMC的一个法向量为
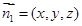 ,则
,则 ,
,令y="1," 则
 ,得平面AMC的一个法向量
,得平面AMC的一个法向量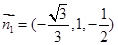 ;(8分)
;(8分)设平面ANC的法向量为
 ,则
,则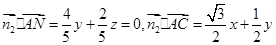 ,
,令y="1," 得平面ANC的一个法向量
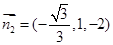 (10分)
(10分)设二面角M-AC-N的平面角为
 ,由图像知其必为锐角,从而有(12分)
,由图像知其必为锐角,从而有(12分)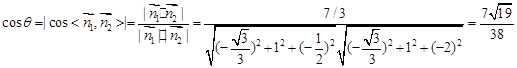 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
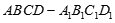 ,
,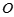 是底
是底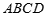 对角线的交点.
对角线的交点.
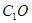 ∥面
∥面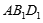 ;
;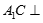 面
面 中
中
 与
与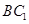 所成角的大小.
所成角的大小. 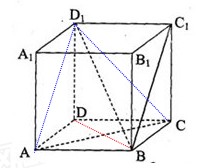
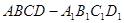 中,
中, 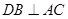 ,点
,点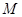 是棱
是棱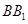 上一点.
上一点.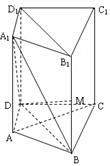
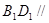 面
面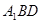 ;
;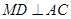 ;
;
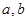 是两条直线,
是两条直线,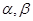 是两个平面,则下列4组条件中:①
是两个平面,则下列4组条件中:①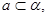
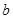 ∥
∥ ,
,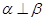 ;②
;②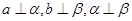 ;③
;③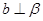 ,
,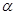 ∥
∥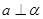 ,
,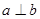 的条件有( )组。
的条件有( )组。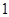
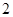
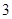
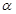 内的一条直线
内的一条直线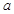 垂直与平面
垂直与平面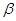 内的无数条直线,则
内的无数条直线,则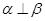
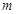 与平面
与平面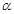 内的一条直线平行,则
内的一条直线平行,则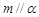
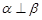 ,且
,且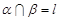 ,则过
,则过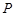 与
与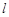 垂直的直线垂直于平面
垂直的直线垂直于平面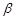
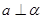 .
. 与平面
与平面 平行的是( )
平行的是( )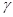
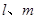 是
是