题目内容
4.如图:二面角α-l-β的大小是60°,线段AB?α,B∈l,AB与l所成角为45°,则AB与平面β所成角的正弦值是$\frac{\sqrt{6}}{4}$.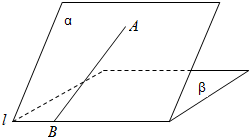
分析 根据二面角和直线和平面所成角的定义,先作出对应的平面角,结合三角形的边角关系进行求解即可.
解答 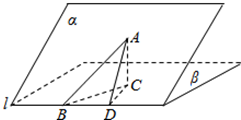 解:过点A作平面β的垂线,垂足为C,在β内过C作l的垂线,垂足为D.
解:过点A作平面β的垂线,垂足为C,在β内过C作l的垂线,垂足为D.
连结AD,根据三垂线定理可得AD⊥l,
因此,∠ADC为二面角α-l-β的平面角,∠ADC=60°
又∵AB与l所成角为45°,
∴∠ABD=45°
连结BC,可得BC为AB在平面β内的射影,
∴∠ABC为AB与平面β所成的角.
设AD=2x,则Rt△ACD中,AC=ADsin60°=$\sqrt{3}x$,
Rt△ABD中,AB=$\frac{AD}{sin45°}=2\sqrt{2}x$,
∴Rt△ABC中,sin∠ABC=$\frac{AC}{AB}=\frac{\sqrt{3}x}{2\sqrt{2}x}$=$\frac{\sqrt{6}}{4}$,
故答案为:$\frac{\sqrt{6}}{4}$.
点评 本题主要考查线面垂直的定义与性质、二面角的平面角的定义和直线与平面所成角的定义及求法等知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.某校高中三个年级共有学生1800名,各年级男生、女生的人数如表:
已知在高中学生中随机抽取一名同学时,抽到高三年级女生的概率为0.17.
(1)求a的值;
(2)现用分层抽样的方法在全校抽取60名学生,则在高二年级应抽取多少名学生?
(3)已知b≥260,c≥200,求高二年级男生比女生多的概率.
| 高一年级 | 高二年级 | 高三年级 | |
| 男生 | 290 | b | 344 |
| 女生 | 260 | c | a |
(1)求a的值;
(2)现用分层抽样的方法在全校抽取60名学生,则在高二年级应抽取多少名学生?
(3)已知b≥260,c≥200,求高二年级男生比女生多的概率.
20.已知变量x和y满足关系y=0.1x-10,变量z与y负相关,则下列结论中正确的是( )
| A. | x与y负相关,x与z负相关 | B. | x与y正相关,x与z正相关 | ||
| C. | x与y正相关,x与z负相关 | D. | x与y负相关,x与z正相关 |
16.过点$P(-\sqrt{3},-1)$的直线l与圆x2+y2=1有两个不同的公共点,则直线l的斜率的取值范围是( )
| A. | $(0,\frac{{\sqrt{3}}}{3})$ | B. | $[0,\sqrt{3}]$ | C. | $[\frac{{\sqrt{3}}}{3},\sqrt{3})$ | D. | $(0,\sqrt{3})$ |