ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§Ά÷‘≤
÷–Θ§Ά÷‘≤![]() ΘΚ
ΘΚ ![]() Θ®
Θ®![]() Θ©ΒΡάκ–Ρ¬ ΈΣ
Θ©ΒΡάκ–Ρ¬ ΈΣ![]() Θ§Ν§Ϋ”Ά÷‘≤
Θ§Ν§Ϋ”Ά÷‘≤![]() ΒΡΥΡΗωΕΞΒψΥυ–Έ≥…ΒΡΥΡ±Ώ–ΈΟφΜΐΈΣ
ΒΡΥΡΗωΕΞΒψΥυ–Έ≥…ΒΡΥΡ±Ώ–ΈΟφΜΐΈΣ![]() Θ°
Θ°

Θ®1Θ©«σΆ÷‘≤![]() ΒΡ±ξΉΦΖΫ≥ΧΘΜ
ΒΡ±ξΉΦΖΫ≥ΧΘΜ
Θ®2Θ©»τΆ÷‘≤![]() …œΒψ
…œΒψ![]() ΒΫΕ®Βψ
ΒΫΕ®Βψ![]() Θ®
Θ®![]() Θ©ΒΡΨύάκΒΡΉν–Γ÷ΒΈΣ1Θ§«σ
Θ©ΒΡΨύάκΒΡΉν–Γ÷ΒΈΣ1Θ§«σ![]() ΒΡ÷ΒΦΑΒψ
ΒΡ÷ΒΦΑΒψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
Θ®3Θ©»γΆΦΘ§ΙΐΆ÷‘≤![]() ΒΡœ¬ΕΞΒψΉςΝΫΧθΜΞœύ¥Ι÷±ΒΡ÷±œΏΘ§Ζ÷±πΫΜΆ÷‘≤
ΒΡœ¬ΕΞΒψΉςΝΫΧθΜΞœύ¥Ι÷±ΒΡ÷±œΏΘ§Ζ÷±πΫΜΆ÷‘≤![]() ”ΎΒψ
”ΎΒψ![]() Θ§
Θ§ ![]() Θ§…η÷±œΏ
Θ§…η÷±œΏ![]() ΒΡ–±¬ ΈΣ
ΒΡ–±¬ ΈΣ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ΘΚ
ΘΚ ![]() Ζ÷±π”κ÷±œΏ
Ζ÷±π”κ÷±œΏ![]() Θ§
Θ§ ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§
Θ§ ![]() Θ°Φ«
Θ°Φ«![]() Θ§
Θ§ ![]() ΒΡΟφΜΐΖ÷±πΈΣ
ΒΡΟφΜΐΖ÷±πΈΣ![]() Θ§
Θ§ ![]() Θ§ «Ζώ¥φ‘Ύ÷±œΏ
Θ§ «Ζώ¥φ‘Ύ÷±œΏ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() ΘΩ»τ¥φ‘ΎΘ§«σ≥ωΥυ”–÷±œΏ
ΘΩ»τ¥φ‘ΎΘ§«σ≥ωΥυ”–÷±œΏ![]() ΒΡΖΫ≥ΧΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
ΒΡΖΫ≥ΧΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ®2Θ©
Θ®2Θ©![]() ΒΡ÷ΒΈΣ2Θ§Βψ
ΒΡ÷ΒΈΣ2Θ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ®3Θ©
Θ®3Θ©![]() Θ§
Θ§ ![]()
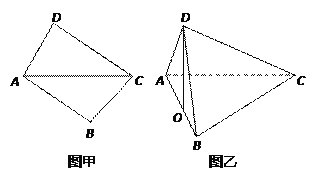
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίΧβ“βΝ–≥ω ΫΉ” ΫβΒΟ
ΫβΒΟ ¥”ΕχΒΟΒΫΆ÷‘≤ΖΫ≥ΧΘΜΘ®2Θ©ΗυΨίΒψΒψΨύΙΪ ΫΒΟΒΫ
¥”ΕχΒΟΒΫΆ÷‘≤ΖΫ≥ΧΘΜΘ®2Θ©ΗυΨίΒψΒψΨύΙΪ ΫΒΟΒΫ![]() Θ§―–ΨΩ’βΗωΚ· ΐΒΡΉν÷ΒΦ¥Ω…ΘΜΘ®3Θ©ΝΣΝΔ÷±œΏΚΆΆ÷‘≤ΒΟΒΫΕΰ¥ΈΖΫ≥ΧΘ§
Θ§―–ΨΩ’βΗωΚ· ΐΒΡΉν÷ΒΦ¥Ω…ΘΜΘ®3Θ©ΝΣΝΔ÷±œΏΚΆΆ÷‘≤ΒΟΒΫΕΰ¥ΈΖΫ≥ΧΘ§  Θ§ΫΪΟφΜΐ±»ΉΣΜ·ΈΣΉχ±ξ÷°±»¥ζ»κΦ¥Ω…ΓΘ
Θ§ΫΪΟφΜΐ±»ΉΣΜ·ΈΣΉχ±ξ÷°±»¥ζ»κΦ¥Ω…ΓΘ
ΫβΈωΘΚ
Θ®1Θ©”…Χβ“βΒΟΘΚ  ΫβΒΟ
ΫβΒΟ
Υυ“‘Ά÷‘≤![]() ΒΡ±ξΉΦΖΫ≥ΧΈΣ
ΒΡ±ξΉΦΖΫ≥ΧΈΣ![]() Θ°
Θ°
Θ®2Θ©…η![]() Θ§”…Ε®Βψ
Θ§”…Ε®Βψ![]() Θ§ΩΦ¬«ΨύάκΒΡΤΫΖΫΘΚ
Θ§ΩΦ¬«ΨύάκΒΡΤΫΖΫΘΚ
‘ρ Θ§
Θ§
Εΰ¥ΈΚ· ΐΒΡΆΦœσΕ‘≥Τ÷αΈΣ![]() Θ§
Θ§
”…Ά÷‘≤ΖΫ≥Χ÷Σ![]() Θ§
Θ§
”…Χβ…η÷Σ![]() Θ§
Θ§
ΔΌΒ±![]() Θ§Φ¥
Θ§Φ¥![]() ±Θ§‘Ύ
±Θ§‘Ύ![]() ±”–
±”–![]() Θ§
Θ§
ΫβΒΟ![]() Θ§≤ΜΖϊΚœΧβ“βΘ§…α»ΞΘΜ
Θ§≤ΜΖϊΚœΧβ“βΘ§…α»ΞΘΜ
ΔΎΒ±![]() Θ§Φ¥
Θ§Φ¥![]() ±Θ§”…ΒΞΒς–‘÷ΣΘΚ‘Ύ
±Θ§”…ΒΞΒς–‘÷ΣΘΚ‘Ύ![]() ±”–
±”–![]() Θ§
Θ§
ΫβΒΟ![]() Μρ
Μρ![]() Θ®…αΘ©Θ°
Θ®…αΘ©Θ°
Ήέ…œΩ…ΒΟΘΚ ![]() ΒΡ÷ΒΈΣ2Θ§Βψ
ΒΡ÷ΒΈΣ2Θ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ°
Θ°
Θ®3Θ©”…Θ®1Θ©÷ΣΘ§ ![]() Θ§‘ρ÷±œΏ
Θ§‘ρ÷±œΏ![]() ΒΡΖΫ≥ΧΈΣ
ΒΡΖΫ≥ΧΈΣ![]() Θ§
Θ§
ΝΣΝΔ œϊ»Ξ
œϊ»Ξ![]() ≤Δ’ϊάμΒΟ
≤Δ’ϊάμΒΟ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() ΘΜ
ΘΜ
÷±œΏ![]() ΒΡΖΫ≥ΧΈΣ
ΒΡΖΫ≥ΧΈΣ![]() Θ§Ά§άμΩ…ΒΟ
Θ§Ά§άμΩ…ΒΟ![]() Θ°
Θ°
ΝΣΝΔ ΫβΒΟ
ΫβΒΟ![]() Θ§Ά§άμΩ…ΒΟ
Θ§Ά§άμΩ…ΒΟ![]() Θ§
Θ§
Υυ“‘ Θ§
Θ§
Φ¥![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Μρ
Μρ![]() Θ§
Θ§
Υυ“‘![]() Μρ
Μρ![]() Θ§
Θ§
Ι ¥φ‘Ύ÷±œΏ![]() ΘΚ
ΘΚ ![]() Θ§
Θ§ ![]() ¬ζΉψΧβ“βΘ°
¬ζΉψΧβ“βΘ°