题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求直线
,求直线![]() 以及曲线
以及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() ,
,![]() (2)
(2)![]()
【解析】
(1)根据![]() 的大小消去参数
的大小消去参数![]() ,求得直线
,求得直线![]() 的直角坐标方程,利用极坐标和直角坐标转化公式,求得曲线
的直角坐标方程,利用极坐标和直角坐标转化公式,求得曲线![]() 的直角坐标方程.(2)方法1:写出直线
的直角坐标方程.(2)方法1:写出直线![]() 的极坐标方程,代入曲线
的极坐标方程,代入曲线![]() 的极坐标方程,根据极坐标系下的弦长公式列方程由此求得直线
的极坐标方程,根据极坐标系下的弦长公式列方程由此求得直线![]() 的斜率.方法2:设出直线的直角坐标方程,联立直线的方程和曲线
的斜率.方法2:设出直线的直角坐标方程,联立直线的方程和曲线![]() 的直角坐标方程,利用弦长公式列方程,解方程求得直线斜率.
的直角坐标方程,利用弦长公式列方程,解方程求得直线斜率.
解:(1)由题意,直线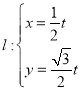 ,可得直线
,可得直线![]() 是过原点的直线,
是过原点的直线,
故其直角坐标方程为![]() ,
,
又![]() ,由
,由![]()
故![]() ;
;
(2)由题意,直线l的极坐标为![]() ,
,
设![]() 、
、![]() 对应的极径分别为
对应的极径分别为![]() ,
,![]()
将![]() 代入曲线
代入曲线![]() 的极坐标可得:
的极坐标可得:
![]() ,
,
故![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,
故![]() ,则
,则![]() ,即
,即![]() ,
,![]() ,
,
所以![]() 故直线
故直线![]() 的斜率是
的斜率是![]()
法二:由题意,直线![]() 方程为
方程为![]() ,设
,设![]() 、
、![]() 对应的点坐标为
对应的点坐标为![]()
联立直线![]() 与曲线
与曲线![]() 的方程
的方程![]() ,消去
,消去![]() 得
得![]() .
.
![]()
![]()
所以![]() ,故直线
,故直线![]() 的斜率是
的斜率是![]() .
.

【题目】每年春晚都是万众瞩目的时刻,这些节目体现的文化内涵、历史背景等反映了社会的进步.国家的富强,人民生活水平的提高等.某学校高三年级主任开学初为了解学生在看春晚后对节目体现的文化内涵、历史背景等是否会在今年的高考题中体现进行过思考,特地随机抽取100名高三学生(其中文科学生50,理科学生50名),进行了调查.统计数据如表所示(不完整):
“思考过” | “没有思考过” | 总计 | |
文科学生 | 40 | 10 | |
理科学生 | 30 | ||
总计 | 100 |
(1)补充完整所给表格,并根据表格数据计算是否有![]() 的把握认为看春晚后会思考节目体现的文化内涵、历史背景等与文理科学生有关;
的把握认为看春晚后会思考节目体现的文化内涵、历史背景等与文理科学生有关;
(2)①现从上表的”思考过”的文理科学生中按分层抽样选出7人.再从这7人中随机抽取4人,记这4人中“文科学生”的人数为![]() ,试求
,试求![]() 的分布列与数学期望;
的分布列与数学期望;
②现设计一份试卷(题目知识点来自春晚相关知识整合与变化),假设“思考过”的学生及格率为![]() ,“没有思考过”的学生的及格率为
,“没有思考过”的学生的及格率为![]() .现从“思考过”与“没有思考过”的学生中分别随机抽取一名学生进行测试,求两人至少有一个及格的概率.
.现从“思考过”与“没有思考过”的学生中分别随机抽取一名学生进行测试,求两人至少有一个及格的概率.
附参考公式: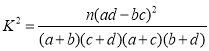 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |