题目内容
【题目】如图，在三棱锥
中，
，
，
，
，
，且
在平面
上的射影
在线段
上．
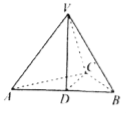
（Ⅰ）求证：
；
（Ⅱ）设二面角
为
，求
的余弦值．
【答案】（Ⅰ）详见解析（Ⅱ）
【解析】
试题分析：（Ⅰ）证明线线垂直，一般利用线面垂直性质定理进行论证；因为
在平面
上的射影
在线段
上，所以
，又根据勾股定理可得
，因此
（Ⅱ）求二面角，一般方法为利用空间向量，即先根据题意建立空间直角坐标系，设立各点坐标，利用方程组解出各面法向量，再根据向量数量积求法向量夹角，最后根据二面角与法向量之间相等或互补的关系求二面角
试题解析：（Ⅰ）证明：
，
，
，
，
，
．
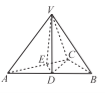
（Ⅱ）解：（法一）作
垂足为
，连接
，
则
为二面角
的平面角．
在
中，
，
，
，
，
，
，
在
中，
，
，
，
，又
，
，又
，
，
．
（法二）在
中，
，
，
，
，
，
，
在
中，
，
，
又
，
，又，
，
如图建立直角坐标系，
，
，
，
，
平面
的法向量为
，
平面
的法向量为
，
．
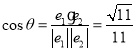优学名师名题系列答案
【题目】某快递公司收取快递费用的标准是：重量不超过
的包裹收费
元；重量超过
的包裹，除
收费
元之外，超过
的部分，每超出
（不足
，按
计算）需再收
元.该公司将最近承揽的
件包裹的重量统计如下：
包裹重量（单位： |
|
|
|
|
|
包裹件数 |
|
|
|
|
|
公司对近
天，每天揽件数量统计如下表：
包裹件数范围 |
|
|
|
|
|
包裹件数 （近似处理） |
|
|
|
|
|
天数 |
|
|
|
|
|
以上数据已做近似处理，并将频率视为概率.
（1）计算该公司未来
天内恰有
天揽件数在
之间的概率；
（2）（i）估计该公司对每件包裹收取的快递费的平均值；
（ii）公司将快递费的三分之一作为前台工作人员的工资和公司利润，剩余的用作其他费用.目前前台有工作人员
人，每人每天揽件不超过
件，工资
元.公司正在考虑是否将前台工作人员裁减
人，试计算裁员前后公司每日利润的数学期望，并判断裁员是否对提高公司利润更有利？
【题目】如表中数表为“森德拉姆筛”，其特点是每行每列都成等差数列，记第i行，第j列的数为aij，则数字41在表中出现的次数为（ ）
2 | 3 | 4 | 5 | 6 | 7 | … |
3 | 5 | 7 | 9 | 11 | 13 | … |
4 | 7 | 10 | 13 | 16 | 19 | … |
5 | 9 | 13 | 17 | 21 | 25 | … |
6 | 11 | 16 | 21 | 26 | 31 | … |
7 | 13 | 19 | 25 | 31 | 37 | … |
… | … | … | … | … | … | … |
A.4B.8C.9D.12
