题目内容
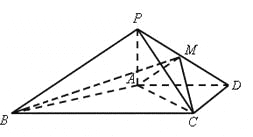
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上.
上.
(1)求证:![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析;(2)![]()
【解析】
试题第一问应用空间的垂直关系的转换,应用线面垂直得出线线垂直的
关系,第二问根据所给的二面角的大小,结合空间向量,从而确定出
点![]() 的位置,再用空间向量确定出线面角的正弦值.
的位置,再用空间向量确定出线面角的正弦值.
试题解析:(Ⅰ)如图,设![]() 为
为![]() 的中点,连结
的中点,连结![]() ,则
,则![]() ,所以四边形
,所以四边形![]() 为平行四边形,
为平行四边形,
故![]() ,又
,又![]() ,
,
所以![]() ,故
,故![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
且![]() ,所以
,所以![]() 平面
平面![]() ,故有
,故有![]()
![]() 分
分
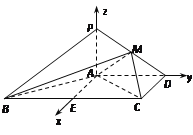
(Ⅱ)如图,以![]() 为原点,分别以射线
为原点,分别以射线![]() 为
为![]() 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系![]() .
.
则![]() ,
,
设![]() ,易得
,易得![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则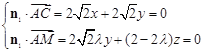 ,
,
令![]() 得
得![]() ,即
,即![]() .
.
又平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由题知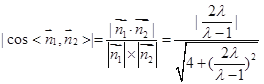
![]() ,解得
,解得![]() ,
,
即![]() ,而
,而![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则![]() .
.
故直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.![]() 分
分

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
【题目】如表中数表为“森德拉姆筛”,其特点是每行每列都成等差数列,记第i行,第j列的数为aij,则数字41在表中出现的次数为( )
2 | 3 | 4 | 5 | 6 | 7 | … |
3 | 5 | 7 | 9 | 11 | 13 | … |
4 | 7 | 10 | 13 | 16 | 19 | … |
5 | 9 | 13 | 17 | 21 | 25 | … |
6 | 11 | 16 | 21 | 26 | 31 | … |
7 | 13 | 19 | 25 | 31 | 37 | … |
… | … | … | … | … | … | … |
A.4B.8C.9D.12

