题目内容
【题目】如图所示,在三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点.
的中点.
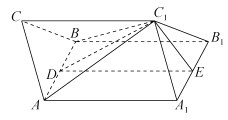
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
【答案】(1)见证明(2)![]()
【解析】
(1)本题首先可借助题目所给出的条件证得![]() 以及
以及![]() ,然后根据线面垂直的判定即可证得
,然后根据线面垂直的判定即可证得![]() 平面
平面![]() ;
;
(2)本题首先可以做![]() 于点
于点![]() ,然后借助(1)中结论证得
,然后借助(1)中结论证得![]() 为四棱锥
为四棱锥![]() 的高,再然后通过题意计算得底面矩形
的高,再然后通过题意计算得底面矩形![]() 的面积以及高
的面积以及高![]() 的长,最后通过四棱锥的体积计算公式即可得出结果。
的长,最后通过四棱锥的体积计算公式即可得出结果。
(1)在三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() ,故
,故![]() ,
,
因为![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)作![]() 于点
于点![]() ,
,
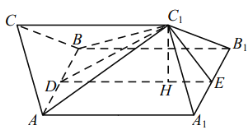
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 为四棱锥
为四棱锥![]() 的高,
的高,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点,所以
的中点,所以![]() ,且
,且![]() ,
,
故四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,且
,且![]() ,
,
所以![]() ,即四边形
,即四边形![]() 为矩形,
为矩形,
因为![]() ,
,![]() ,所以矩形
,所以矩形![]() 的面积
的面积![]() ,
,
因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,故
,故![]() ,
,
所以四棱锥![]() 的体积
的体积![]() .
.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目