题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,证明:
时,证明: ![]() (其中e为自然对数的底数).
(其中e为自然对数的底数).
【答案】(1)当![]() 时,
时, ![]() 的递增区间为
的递增区间为![]() ;
;
当![]() 时,
时,![]() 的递增区间为
的递增区间为![]() ,
,![]() ,递减区间为
,递减区间为![]() ;
;
当![]() 时,
时,![]() 的递增区间为
的递增区间为![]() ,
,![]() ,递减区间为
,递减区间为![]() ;
;
(2)见解析
【解析】
(1)求出函数的导数,通过讨论![]() 的取值范围,求出函数的单调区间即可.
的取值范围,求出函数的单调区间即可.
(2)问题转化为![]() ,令
,令![]()
![]() ,根据函数的单调性证明即可.
,根据函数的单调性证明即可.
(1)由题意,函数![]() 的定义域为
的定义域为![]() ,
,
![]()
当![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 的递增区间为
的递增区间为![]() ;
;
当![]() 时,在区间
时,在区间![]() ,
,![]() 时
时![]() ,
,![]() 时
时![]() ,
,
所以![]() 的递增区间为
的递增区间为![]() ,
,![]() ,递减区间为
,递减区间为![]() ;
;
当![]() 时,在区间
时,在区间![]() ,
,![]() 时
时![]() ,
,![]() 时
时![]() ,
,
所以![]() 的递增区间为
的递增区间为![]() ,
,![]() ,递减区间为
,递减区间为![]() ;
;
综上所述,当![]() 时,
时, ![]() 的递增区间为
的递增区间为![]() ;
;
当![]() 时,
时,![]() 的递增区间为
的递增区间为![]() ,
,![]() ,递减区间为
,递减区间为![]() ;
;
当![]() 时,
时,![]() 的递增区间为
的递增区间为![]() ,
,![]() ,递减区间为
,递减区间为![]() ;
;
(2)当![]() 时,由
时,由![]() ,只需证明
,只需证明![]() .
.
令![]()
![]() ,
,![]() .
.
设![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
∴当![]() 时,
时,![]() 取得唯一的极小值,也是最小值.
取得唯一的极小值,也是最小值.
![]() 的最小值是
的最小值是![]()
![]() 成立.
成立.
故![]() 成立.
成立.

【题目】某公司为了确定下一年度投入某种产品的宣传费用,需了解年宣传费![]() (单位:万元)对年销量
(单位:万元)对年销量![]() (单位:吨)和年利润(单位:万元)的影响对近6年宣传费
(单位:吨)和年利润(单位:万元)的影响对近6年宣传费![]() 和年销量
和年销量![]() 的数据做了初步统计,得到如下数据:
的数据做了初步统计,得到如下数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年宣传费 | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() ,两边取对数,即
,两边取对数,即![]() ,令
,令![]() ,即
,即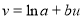 对上述数据作了初步处理,得到相关的值如下表:
对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(1)从表中所给出的6年年销售量数据中任选2年做年销售量的调研,求所选数据中至多有一年年销售量低于21吨的概率.
(2)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若生产该产品的固定成本为200(万元),且每生产1(吨)产品的生产成本为20(万元)(总成本=固定成本+生产成本+年宣传费),销售收入为![]() (万元),假定该产品产销平衡(即生产的产品都能卖掉),2019年该公司计划投入108万元宣传费,你认为该决策合理吗?请说明理由.(其中
(万元),假定该产品产销平衡(即生产的产品都能卖掉),2019年该公司计划投入108万元宣传费,你认为该决策合理吗?请说明理由.(其中![]() 为自然对数的底数,
为自然对数的底数,![]() )
)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为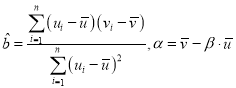
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
【题目】为了解中学生对交通安全知识的掌握情况,从农村中学和城镇中学各选取100名同学进行交通安全知识竞赛.下图1和图2分别是对农村中学和城镇中学参加竞赛的学生成绩按![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
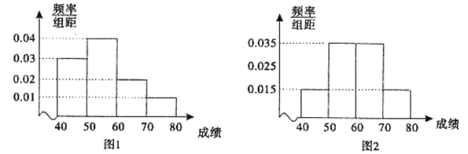
(Ⅰ)分别估算参加这次知识竞赛的农村中学和城镇中学的平均成绩;
(Ⅱ)完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
农村中学 | |||
城镇中学 | |||
合计 |
附:![]()
临界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |