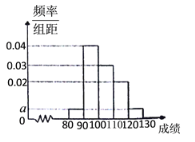
题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)令函数![]() ,若函数
,若函数![]() 有且只有一个零点
有且只有一个零点![]() ,试判断
,试判断![]() 与3的大小,并说明理由.
与3的大小,并说明理由.
【答案】(1)见解析;(2)见解析
【解析】
(1)先求导,然后讨论![]() 的大小,继而求出函数的单调性
的大小,继而求出函数的单调性
(2)对函数![]() 求二阶导数,求出函数
求二阶导数,求出函数![]() 的单调性,然后结合零点得到关于
的单调性,然后结合零点得到关于![]() 的表达式,构造新函数后运用导数确定新函数的单调性,继而得出关于零点问题
的表达式,构造新函数后运用导数确定新函数的单调性,继而得出关于零点问题
(1)![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() 时,
时,![]() ,
,![]() 在上单调递增.
在上单调递增.
②当![]() ,即
,即![]() 时,
时,![]() 时,
时,![]()
![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增.
单调递增.
(2)函数![]() ,
,
则![]() ,令
,令![]()
则![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 且
且![]() 时,
时,![]() ,
,![]() 时
时![]() ,
,
所以![]() 在
在![]() 上有唯一零点,
上有唯一零点,
当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,所以
,所以![]() 为
为![]() 的最小值.
的最小值.
由已知函数![]() 有且只有一个零点
有且只有一个零点![]() ,则
,则![]() ,
,
所以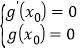 ,
,
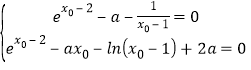
![]()
![]() ,
,
令![]() ,
,
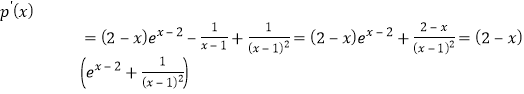 ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() 在
在![]() 单调递减,
单调递减,
因为![]() ,
,![]() ,
,
所以![]() 在
在![]() 上有一个零点,在
上有一个零点,在![]() 无零点,
无零点,
若![]() 在
在![]() 有零点必小于3,
有零点必小于3,
综上:![]() .
.

练习册系列答案
相关题目