题目内容
【题目】从某校参加期中考试的高一学生中随机抽取100名得到这100名学生语文成绩的频率分布直方图如图所示，其中成绩分组区间是：
.
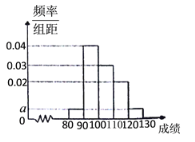
（1）求图中
的值；
（2）根据频率分布直方图，估计这100名学生语文成绩的平均分，众数，中位数；
（3）已知学生
的语文成绩为123分，现从成绩在
中的学生中随机抽取2人参加演讲赛，求学生被抽中的概率.
【答案】(1) 
;(2) 103分,95分,101.67分;(3)
.
【解析】
（1）根据频率之和为1,直接列式计算即可；
（2）平均数等于每组的中间值乘以该组频率,再求和;众数指频率最大的一组的中间值;中位数两端的小长方形面积之和均为0.5;（3）根据题意分别求出
的人数,根据列举的结果即可求得概率.
(1)由频率分布直方图可得：
解得:.
(2)平均分为：
(分).
众数为:
(分).
∵
的频率为
的频率为
∴中位数为：
(分).
(3)成绩在的人数为
(人).设另外4人为
,抽取2人共有
,
,
,
,
,
,
,
,
,
10种结果, 学生
被抽中的概率
.
学而优衔接教材南京大学出版社系列答案【题目】为提高玉米产量，某种植基地对单位面积播种数与每棵作物的产量之间的关系进行了研究，收集了
块试验田的数据，得到下表：
试验田编号 |
|
|
|
|
|
|
|
|
|
|
|
（棵/） |
|
|
|
|
|
|
|
|
|
|
|
（斤/棵） |
|
|
|
|
|
|
|
|
|
|
|
技术人员选择模型
作为
与
的回归方程类型，令
，
相关统计量的值如下表：
|
|
|
|
|
|
|
|
由表中数据得到回归方程后进行残差分析，残差图如图所示：
（1）根据残差图发现一个可疑数据，请写出可疑数据的编号（给出判断即可，不必说明理由）；
（2）剔除可疑数据后，由最小二乘法得到关于的线性回归方程
中的
，求关于
的回归方程；
（3）利用（2）得出的结果，计算当单位面积播种数为何值时，单位面积的总产量
的预报值最大？（计算结果精确到
）
附：对于一组数据
，
，
，
其回归直线
的斜率和截距的最小二乘法估计分别为
，
，
【题目】线段AB外有一点C，∠ABC＝60°，AB＝200 km，汽车以80 km/h的速度由A向B行驶，同时摩托车以50 km/h的速度由B向C行驶，则运动开始________h后，两车的距离最小．
【题目】今年年初，我国多个地区发生了持续性大规模的雾霾天气，给我们的身体健康产生了巨大的威胁．私家车的尾气排放也是造成雾霾天气的重要因素之一，因此在生活中我们应该提倡低碳生活，少开私家车，尽量选择绿色出行方式，为预防雾霾出一份力．为此，很多城市实施了机动车车尾号限行，我市某报社为了解市区公众对“车辆限行”的态度，随机抽查了50人，将调查情况进行整理后制成下表：
年龄（岁） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
（Ⅰ）完成被调查人员的频率分布直方图；
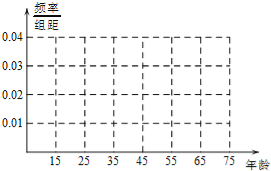
（Ⅱ）若从年龄在[15，25），[25，35）的被调查者中各随机选取两人进行进行追踪调查，记选中的4人中不赞成“车辆限行”的人数为ξ，求随机变量ξ的分布列和数学期望．
