题目内容
【题目】给出以下五个结论:
①函数![]() 是偶函数;
是偶函数;
②当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ;
;
③等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]() ;
;
④已知定义域为![]() 的函数
的函数![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 成立.
成立.
![]() 函数
函数![]() 的最小值4;
的最小值4;
则上述结论中正确的是______(写出所有正确结论的序号).
【答案】②③④
【解析】
利用特殊值代入①中的解析式即可判断①;根据函数单调性及自变量取值范围,可判断②;讨论![]() 的符号去绝对值,即可判断④;换元得
的符号去绝对值,即可判断④;换元得![]() ,利用函数单调性即可判断⑤.
,利用函数单调性即可判断⑤.
当![]() 与
与![]() 时,代入①中的解析式所得函数值不相等,所以①错误;
时,代入①中的解析式所得函数值不相等,所以①错误;
当![]() 时,
时,![]() ,由余弦函数图象可知
,由余弦函数图象可知![]() 的值域是
的值域是![]() ,所以②正确;
,所以②正确;
设![]() ,故③正确;
,故③正确;
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,
![]() ,当
,当![]() 时,
时,
![]() ,综上,
,综上,![]() 时,
时,![]() ,所以④正确.
,所以④正确.
⑤设![]() ,所以函数g(t)在
,所以函数g(t)在![]() 上单调递减,所以函数的最小值为g(1)=5,所以该命题是假命题.
上单调递减,所以函数的最小值为g(1)=5,所以该命题是假命题.
故答案为:②③④.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
【题目】今年年初,我国多个地区发生了持续性大规模的雾霾天气,给我们的身体健康产生了巨大的威胁.私家车的尾气排放也是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(Ⅰ)完成被调查人员的频率分布直方图;
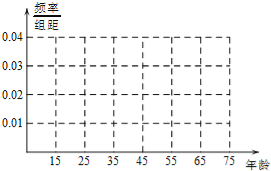
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望.