题目内容
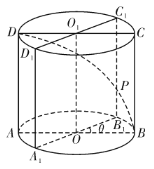
【题目】如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠APC＝90°，∠BPD＝120°，PB＝PD．
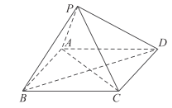
（1）求证：平面APC⊥平面BPD；
（2）若AB＝2AP＝2，求三棱锥C-PBD的体积．
【答案】（1）详见解析；（2）
．
【解析】
（1）记
与
交点为
，利用
，
证得线面垂直，从而可证得面面垂直；
（2）设
，利用
求得
，从而得
的长度，过
作
，垂足为
，由（1）可证
就是四棱锥的高，求出这个高及底面面积, 用换底法可得体积．
（1）证明：记与交点为，∵
，为的中点，∴，又∵
为菱形，∴．
∵和
是平面
内两条相交直线，∴
平面．
又
平面
，∴平面
平面．
（2）设，∵
，∴
，又
，所以
，所以
，因为
，所以在中，由勾股定理得
，
，∴
，∴
．
过作，垂足为，由（1）知，平面，∴平面平面．又平面
平面
，所以
平面．
在
中，得
，所以三棱锥
的体积
．
练习册系列答案
名校课堂系列答案
相关题目
【题目】今年年初，我国多个地区发生了持续性大规模的雾霾天气，给我们的身体健康产生了巨大的威胁．私家车的尾气排放也是造成雾霾天气的重要因素之一，因此在生活中我们应该提倡低碳生活，少开私家车，尽量选择绿色出行方式，为预防雾霾出一份力．为此，很多城市实施了机动车车尾号限行，我市某报社为了解市区公众对“车辆限行”的态度，随机抽查了50人，将调查情况进行整理后制成下表：
年龄（岁） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
（Ⅰ）完成被调查人员的频率分布直方图；
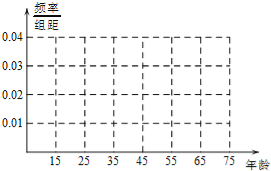
（Ⅱ）若从年龄在[15，25），[25，35）的被调查者中各随机选取两人进行进行追踪调查，记选中的4人中不赞成“车辆限行”的人数为ξ，求随机变量ξ的分布列和数学期望．
