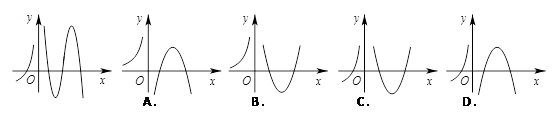题目内容
设函数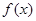 在定义域内可导,
在定义域内可导,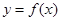 的图象如下左图所示,则导函数
的图象如下左图所示,则导函数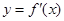 的图象可能是( )
的图象可能是( )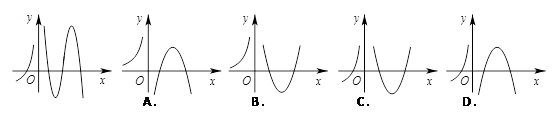
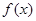 在定义域内可导,
在定义域内可导,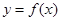 的图象如下左图所示,则导函数
的图象如下左图所示,则导函数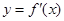 的图象可能是( )
的图象可能是( )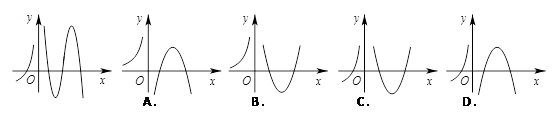
A
试题分析:y轴左侧,函数的图象上升,说明函数为增函数,导数应为正数,排除C,D;y轴右侧,函数图象先降后升,说明函数先减后增,导数值应是先负后正,故选A。
点评:简单题,在某区间,导数值非负,函数为增函数,导数值非正,函数为减函数。

练习册系列答案
相关题目
题目内容
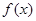 在定义域内可导,
在定义域内可导,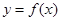 的图象如下左图所示,则导函数
的图象如下左图所示,则导函数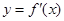 的图象可能是( )
的图象可能是( )