题目内容
2.已知$\frac{z-1}{z+1}$为纯虚数,且(z+1)($\overline{z}$+1)=|z|2,求复数z.分析 设$\frac{z-1}{z+1}$=mi(m∈R且m≠0),求出复数z,代入(z+1)($\overline{z}$+1)=|z|2求得m的值,则复数z可求.
解答 解:设$\frac{z-1}{z+1}$=mi(m∈R且m≠0),则$z=\frac{1-{m}^{2}}{1+{m}^{2}}+\frac{2mi}{1+{m}^{2}}$,
又(z+1)($\overline{z}$+1)=|z|2,得$|z{|}^{2}+z+\overline{z}+1=|z{|}^{2}$,
∴z+$\overline{z}=1$,即$\frac{2-2{m}^{2}}{1+{m}^{2}}=1$,解得:$m=±\frac{\sqrt{3}}{3}$.
当m=$\frac{\sqrt{3}}{3}$时,$z=\frac{1-\frac{1}{3}}{1+\frac{1}{3}}+\frac{\frac{2\sqrt{3}}{3}i}{\frac{4}{3}}=\frac{1}{2}+\frac{\sqrt{3}}{2}i$;
当m=$-\frac{\sqrt{3}}{3}$时,$z=\frac{1}{2}-\frac{\sqrt{3}}{2}i$.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,考查了复数相等的条件,是基础的计算题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
14. 如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )
如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )
 如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )
如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )| A. | (1,$\sqrt{2}$) | B. | (1,2) | C. | ($\sqrt{2}$,+∞) | D. | (2,+∞) |
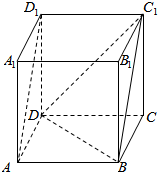 如图,在正方形ABCD-A1B1C1D1中,
如图,在正方形ABCD-A1B1C1D1中,