题目内容
6.对于任意的三个正数a,b,c,求证:a+b+c≥$\sqrt{ab}$+$\sqrt{bc}$+$\sqrt{ca}$,并指出等号成立的条件.分析 由正数a,b,c,运用基本不等式a+b≥2$\sqrt{ab}$,b+c≥2$\sqrt{bc}$,c+a≥2$\sqrt{ca}$,相加即可得证,且a=b=c,取得等号.
解答 证明:任意的三个正数a,b,c,
由a+b≥2$\sqrt{ab}$,
b+c≥2$\sqrt{bc}$,
c+a≥2$\sqrt{ca}$,
相加可得,
a+b+c≥$\sqrt{ab}$+$\sqrt{bc}$+$\sqrt{ca}$.
当且仅当a=b=c,取得等号.
点评 本题考查不等式的证明,考查基本不等式的运用,考查推理能力,属于基础题.

练习册系列答案
相关题目
14. 如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )
如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )
 如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )
如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )| A. | (1,$\sqrt{2}$) | B. | (1,2) | C. | ($\sqrt{2}$,+∞) | D. | (2,+∞) |
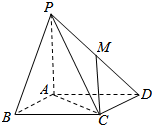 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=AB,点M在棱PD上,PB∥平面ACM.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=AB,点M在棱PD上,PB∥平面ACM. 平面α内有△ABC,AB=5,BC=8,AC=7,梯形BCDE的底DE=2,过EB的中点B1的平面β∥α,若β分别交EA、DC于A1、C1,求△A1B1C1的面积.
平面α内有△ABC,AB=5,BC=8,AC=7,梯形BCDE的底DE=2,过EB的中点B1的平面β∥α,若β分别交EA、DC于A1、C1,求△A1B1C1的面积.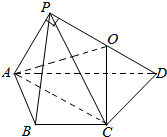 如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=2,PD=2$\sqrt{3}$,PA⊥PD,Q为PD的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=2,PD=2$\sqrt{3}$,PA⊥PD,Q为PD的中点. 如图,四边形ABCD是矩形,四边形BCEF是直角梯形,平面ABCD⊥平面BCEF,∠FBC是直角,AB=1,BC=BF=2,CE=4,P、Q、R分别是AF、DF、DE的中点.
如图,四边形ABCD是矩形,四边形BCEF是直角梯形,平面ABCD⊥平面BCEF,∠FBC是直角,AB=1,BC=BF=2,CE=4,P、Q、R分别是AF、DF、DE的中点.