题目内容
7. 如图圆锥的轴截面为等腰直角三角形SAB,Q为底面圆周上一点.
如图圆锥的轴截面为等腰直角三角形SAB,Q为底面圆周上一点.(1)如果QB的中点为C,OH⊥SC,求证:OH⊥平面SBQ;
(2)如果∠AOQ=60°,QB=2$\sqrt{3}$,求圆锥的体积.
分析 (1)如图所示,由OB=OQ,QC=CB,利用等腰三角形的性质可得QB⊥OC.利用线面垂直的性质可得:BQ⊥SO.于是QB⊥平面SOC,可得QB⊥OH.即可证明.
(2)由∠AOQ=60°,可得∠BOQ=120°.又QB=2$\sqrt{3}$,可得OQ=$\frac{QC}{sin6{0}^{°}}$=2.在等腰Rt△SAB中,AB=4,可得SA=SB,SO.利用V圆锥=$\frac{1}{3}π×O{A}^{2}×SO$即可得出.
解答 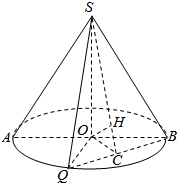 (1)证明:如图所示,
(1)证明:如图所示,
∵OB=OQ,QC=CB,
∴QB⊥OC,
又SO⊥底面OBQ,
∴BQ⊥SO.
又SO∩OC=O,
∴QB⊥平面SOC.
∴QB⊥OH.
又OH⊥SC,SC∩QB=C,
∴OH⊥平面SBQ.
(2)解:∵∠AOQ=60°,∴∠BOQ=120°.
又QB=2$\sqrt{3}$,∴OQ=$\frac{QC}{sin6{0}^{°}}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2.
在等腰Rt△SAB中,AB=4,
∴SA=SB=2$\sqrt{2}$.SO=2.
∴V圆锥=$\frac{1}{3}π×O{A}^{2}×SO$
=$\frac{1}{3}×π×{2}^{2}×2$
=$\frac{8π}{3}$.
点评 本题考查了等腰三角形的性质、直角三角形的性质、线面垂直的判定与性质定理、圆锥的体积计算公式,考查了空间想象能力、推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2$\sqrt{2}$的正方形,PD=4,E,F是PB上的动点,且EF=2.
已知四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2$\sqrt{2}$的正方形,PD=4,E,F是PB上的动点,且EF=2.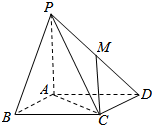 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=AB,点M在棱PD上,PB∥平面ACM.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=AB,点M在棱PD上,PB∥平面ACM.