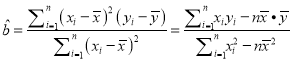题目内容
【题目】某学校高二年级共有1600人，现统计他们某项任务完成时间介于30分钟到90分钟之间，图中是统计结果的频率分布直方图.
（1）求平均值、众数、中位数；
（2）若学校规定完成时间在
分钟内的成绩为
等；完成时间在
分钟内的成绩为
等；完成时间在
分钟内的成绩为
等，按成绩分层抽样从全校学生中抽取10名学生，则成绩为等的学生抽取人数为？
（3）在（2）条件下抽取的成绩为等的学生中再随机选取两人，求两人中至少有一人完成任务时间在
分钟的概率.
【答案】（1）平均数
，众数为55，中位数为
；（2）B中抽7人；
（3）两人中至少有一人完成任务时间在[60，70）分钟的概率为
．
【解析】试题分析：（1）应用条形分布直方图求平均数的公式为
（2）根据系统抽样，按照比例抽得人数
（3）用列举法，将满足条件的例子都写出来，根据离散型随机变量的概率计算公式得到．
（Ⅰ）平均数为；
众数为55；因为完成时间在[30，50)分钟内的频率为0.2，在[50，60)分钟内的频率为0.5，所以中位数为．
（Ⅱ）因为A，B，C的频率比为2︰7︰1，共抽10人，所以B中抽7人．
（Ⅲ）抽出的成绩为B等学生中完成任务时间[50，60)分钟的学生有5人，设为a，b，c，d，e；在[60，70)分钟的学生人数为2人，设为x，y，
则7人中任选两人共有：(a，b)，(a，c)，(a，d)，(a，e)，(a，x)，(a，y)，(b，c)，(b，d)，(b，e)，(b，x)，(b，y)，(c，d)，(c，e)，(c，x)，(c，y)，(d，e)，(d，x)，(d，y)，(e，x)，(e，y)，(x，y)共21种．
两人中至少有一人完成任务时间在[60，70）分钟内的有：(a，x)，(a，y)，(b，x)，(b，y)，(c，x)，(c，y)，(d，x)，(d，y)，(e，x)，(e，y)，(x，y)共11种．
所以两人中至少有一人完成任务时间在[60，70）分钟的概率为．
