题目内容
)袋中装着标有数字1,2,3的小球各2个,从袋中任取2个小球,每个小球被取出的可能性都相等.
(Ⅰ)求取出的2个小球上的数字互不相同的概率;
(Ⅱ)用 表示取出的2个小球上的数字之和,求随机变量
表示取出的2个小球上的数字之和,求随机变量 的概率分布与数学期望.
的概率分布与数学期望.
(Ⅰ)求取出的2个小球上的数字互不相同的概率;
(Ⅱ)用
 表示取出的2个小球上的数字之和,求随机变量
表示取出的2个小球上的数字之和,求随机变量 的概率分布与数学期望.
的概率分布与数学期望.(1) 、(Ⅱ)
、(Ⅱ)
 、(Ⅱ)
、(Ⅱ)
(Ⅰ)解法一:记“取出的2个小球上的数字互不相同”为事件 ,∵从袋中的6个小球中任取2个小球的方法共有
,∵从袋中的6个小球中任取2个小球的方法共有 种,其中取出的2个小球上的数字互不相同的方法有
种,其中取出的2个小球上的数字互不相同的方法有 ,
,
∴ .-------6分
.-------6分
解法二:记“取出的2个小球上的数字互不相同”的事件记为 ,“取出的2个小球上的数字相同”的事件记为
,“取出的2个小球上的数字相同”的事件记为 ,则事件
,则事件 与事件
与事件 是对立事件.∵
是对立事件.∵ ,
,
∴ .------6分
.------6分
(Ⅱ)解:由题意, 所有可能的取值为:2,3,4,5,6.
所有可能的取值为:2,3,4,5,6.
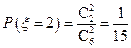 ,
, ,
, ,
,
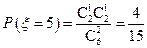 ,
, .
.
故随机变量 的概率分布为:
的概率分布为:
-----------------------------------------------------------------11分
因此, 的数学期望
的数学期望 .---13分
.---13分
 ,∵从袋中的6个小球中任取2个小球的方法共有
,∵从袋中的6个小球中任取2个小球的方法共有 种,其中取出的2个小球上的数字互不相同的方法有
种,其中取出的2个小球上的数字互不相同的方法有 ,
,∴
 .-------6分
.-------6分解法二:记“取出的2个小球上的数字互不相同”的事件记为
 ,“取出的2个小球上的数字相同”的事件记为
,“取出的2个小球上的数字相同”的事件记为 ,则事件
,则事件 与事件
与事件 是对立事件.∵
是对立事件.∵ ,
,∴
 .------6分
.------6分(Ⅱ)解:由题意,
 所有可能的取值为:2,3,4,5,6.
所有可能的取值为:2,3,4,5,6.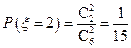 ,
, ,
, ,
,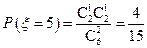 ,
, .
.故随机变量
 的概率分布为:
的概率分布为: | 2 | 3 | 4 | 5 | 6 |
 | 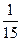 | 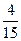 |  | 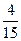 | 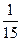 |
因此,
 的数学期望
的数学期望 .---13分
.---13分
练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 ;乙抛掷3次,记正面朝上的次为
;乙抛掷3次,记正面朝上的次为 .(Ⅰ)分别求
.(Ⅰ)分别求 服从以下分布:
服从以下分布:
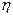 服从二项分布
服从二项分布 .
.

 ,求
,求