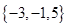题目内容
在一个不透明的纸袋里装有5个大小相同的小球,其中有1个红球和4个黄球,规定每次从袋中任意摸出一球,若摸出的是黄球则不再放回,直到摸出红球为止,求摸球次数ξ的期望和方差.
根据题意可得:ξ可能取的值为1,2,3,4,5,
所以P(ξ=1)=
,P(ξ=2)=
×
=
,P(ξ=3)=
×
×
=
,
P(ξ=4)=
×
×
×
=
,P(ξ=5)=
×
×
×
×1=
,
∴ξ的分布列为
由数学期望的定义知:Eξ=0.2×(1+2+3+4+5)=3(10分),
根据方差的定义可得:Dξ=0.2×(22+12+02+12+22)=2(12分)
所以P(ξ=1)=
| 1 |
| 5 |
| 4 |
| 5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
P(ξ=4)=
| 4 |
| 5 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 5 |
∴ξ的分布列为
| ξ | 1 | 2 | 3 | 4 | 5 |
| P | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
根据方差的定义可得:Dξ=0.2×(22+12+02+12+22)=2(12分)

练习册系列答案
相关题目
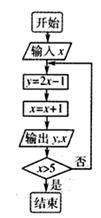
 表示取出的2个小球上的数字之和,求随机变量
表示取出的2个小球上的数字之和,求随机变量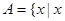 是程序框图中输出的值},集合
是程序框图中输出的值},集合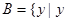 是程序框图中输出的值},全集U=Z,Z为整数集,当
是程序框图中输出的值},全集U=Z,Z为整数集,当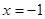 时,
时,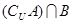 等于( )
等于( )