题目内容
如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC.把△BAC沿AC折起到△PAC的位置,使得点P在平面ADC上的正投影O恰好落在线段AC上,如图2所示.点E、F分别为棱PC,CD的中点.
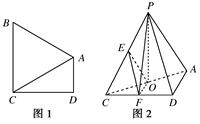
(1)求证:平面OEF∥平面APD;
(2)求证:CD⊥平面POF;
(3)在棱PC上是否存在一点M,使得M到P,O,C,F四点距离相等?请说明理由.

(1)求证:平面OEF∥平面APD;
(2)求证:CD⊥平面POF;
(3)在棱PC上是否存在一点M,使得M到P,O,C,F四点距离相等?请说明理由.
(1)见解析(2)见解析(3)存在
(1)证明:因为点P在平面ADC上的正投影O恰好落在线段AC上,所以PO⊥平面ADC,所以PO⊥AC.
因为AB=BC,所以O是AC的中点,
所以OE∥PA.
同理OF∥AD.
又OE∩OF=O,PA∩AD=A,
所以平面OEF∥平面PDA.
(2)证明:因为OF∥AD,AD⊥CD,
所以OF⊥CD.
又PO⊥平面ADC,CD?平面ADC,
所以PO⊥CD.
又OF∩PO=O,所以CD⊥平面POF.
(3)存在,事实上记点E为M即可.
因为CD⊥平面POF,PF?平面POF,
所以CD⊥PF.
又E为PC的中点,所以EF=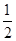 PC,
PC,
同理,在直角三角形POC中,EP=EC=OE=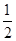 PC,
PC,
所以点E到四个点P,O,C,F的距离相等.
因为AB=BC,所以O是AC的中点,
所以OE∥PA.
同理OF∥AD.
又OE∩OF=O,PA∩AD=A,
所以平面OEF∥平面PDA.
(2)证明:因为OF∥AD,AD⊥CD,
所以OF⊥CD.
又PO⊥平面ADC,CD?平面ADC,
所以PO⊥CD.
又OF∩PO=O,所以CD⊥平面POF.
(3)存在,事实上记点E为M即可.
因为CD⊥平面POF,PF?平面POF,
所以CD⊥PF.
又E为PC的中点,所以EF=
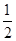 PC,
PC,同理,在直角三角形POC中,EP=EC=OE=
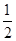 PC,
PC,所以点E到四个点P,O,C,F的距离相等.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 AB=1,M是PB的中点.
AB=1,M是PB的中点.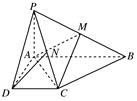
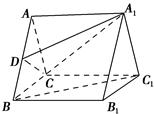
 的侧棱与底面垂直,
的侧棱与底面垂直, ,
, , M、N分别是
, M、N分别是 的中点,点P在线段
的中点,点P在线段 上,且
上,且 ,
,
 取何值,总有
取何值,总有 .
. 时,求平面
时,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值. a
a α;
α;