题目内容
如图，已知四棱锥P－ABCD的底面为直角梯形，AB∥CD，∠DAB＝90°，PA⊥底面ABCD，且PA＝AD＝DC＝
AB＝1，M是PB的中点．
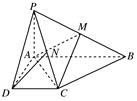
(1)求证：AM＝CM；
(2)若N是PC的中点，求证：DN∥平面AMC.
AB＝1，M是PB的中点．(1)求证：AM＝CM；
(2)若N是PC的中点，求证：DN∥平面AMC.
（1）见解析（2）见解析
(1)在直角梯形ABCD中，AD＝DC＝AB＝1，∴AC＝
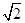，BC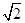＝，∴BC⊥AC，
又PA⊥平面ABCD，BC?平面ABCD，
∴BC⊥PA，∴BC⊥平面PAC，∴BC⊥PC.
在Rt△PAB中，M为PB的中点，则AM＝PB，
在Rt△PBC中，M为PB的中点，则CM＝PB，∴AM＝CM.
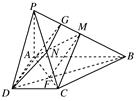
(2)连接DB交AC于点F，
∵DC=AB，∴DF＝FB.
取PM的中点G，连接DG，FM，则DG∥FM，
又DG?平面AMC，FM?平面AMC，
∴DG∥平面AMC.
连接GN，则GN∥MC，
∴GN∥平面AMC，
又GN∩DG＝G，
∴平面DNG∥平面AMC.
又DN?平面DNG，∴DN∥平面AMC.
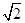AB＝1，∴AC＝，BC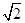＝，∴BC⊥AC，又PA⊥平面ABCD，BC?平面ABCD，
∴BC⊥PA，∴BC⊥平面PAC，∴BC⊥PC.
在Rt△PAB中，M为PB的中点，则AM＝
PB，在Rt△PBC中，M为PB的中点，则CM＝
PB，∴AM＝CM.(2)连接DB交AC于点F，
∵DC=
AB，∴DF＝FB.取PM的中点G，连接DG，FM，则DG∥FM，
又DG?平面AMC，FM?平面AMC，
∴DG∥平面AMC.
连接GN，则GN∥MC，
∴GN∥平面AMC，
又GN∩DG＝G，
∴平面DNG∥平面AMC.
又DN?平面DNG，∴DN∥平面AMC.
练习册系列答案
相关题目
.
.
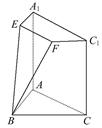
为直角梯形，
,
平面
平面
;
所成锐二面角的余弦值.
均不在平面
内，给出下列命题：
，则
；②若
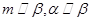，则
，则
，则