题目内容
【题目】在平面直角坐标系xOy中,已知点P(0,1)在圆C:x2+y2+2mx﹣2y+m2﹣4m+1=0内,若存在过点P的直线交圆C于A、B两点,且△PBC的面积是△PAC的面积的2倍,则实数m的取值范围为 .
【答案】( ![]() ,4)
,4)
【解析】解:点P(0,1)在圆C:x2+y2+2mx﹣2y+m2﹣4m+1=0内, ∴1﹣2+m2﹣4m+1<0,
解得0<m<4;
又圆C化为标准方程是(x+m)2+(y﹣1)2=4m,圆心C(﹣m,1);
∵△PBC的面积是△PAC的面积的2倍,
∴PB=2PA,
设直线l的方程为:y=kx+1.
圆心C到直线l的距离d= ![]() =
= ![]() .
.
∴ ![]() =3
=3 ![]() ,可得:9m2﹣4m=10d2=10×
,可得:9m2﹣4m=10d2=10× ![]() ,
,
∴9﹣ ![]() =
= ![]() ∈[0,10),
∈[0,10),
解得: ![]() .
.
当m= ![]() 时,四点共线没有三角形,
时,四点共线没有三角形,
∴实数m的取值范围为( ![]() ,4).
,4).
所以答案是:( ![]() ,4).
,4).
【考点精析】通过灵活运用点与圆的位置关系,掌握点![]() 与圆
与圆![]() 的位置关系有三种:若
的位置关系有三种:若![]() ,则
,则![]() 点
点![]() 在圆外;
在圆外;![]() 点
点![]() 在圆上;
在圆上;![]() 点
点![]() 在圆内即可以解答此题.
在圆内即可以解答此题.

【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了 ![]() 名女性或
名女性或 ![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.
(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过 ![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中 ![]()
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄”45岁为分界点,由以上统计数据完成下面 ![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在 ![]() 和
和 ![]() 的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在
的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在 ![]() 的概率.
的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: ![]() (其中
(其中 ![]() )
)
【题目】电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.
表1
观看方式 | 电视 | 网络 |
| 150 | 250 |
| 120 | 80 |
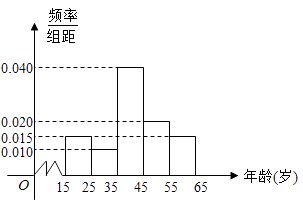
求:(I)假设同一组中的每个数据用该组区间的中点值代替,求非常喜欢《人民的名义》这部电视剧的观众的平均年龄;
(II)根据表1,通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: ![]()