ћвƒњƒЏ»Ё
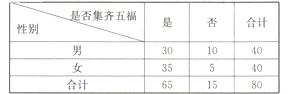
°Њћвƒњ°њЋж„≈ ÷їъµƒЈҐ’є£ђ°∞ќҐ–≈°±‘љјі‘љ≥…ќ™»Ћ√«љїЅчµƒ“ї÷÷Јљ љ.ƒ≥їъєєґ‘°∞ є”√ќҐ–≈љїЅч°±µƒћђґ»љш––µч≤й£ђЋжїъ≥й»°ЅЋ50»Ћ£ђЋы√«ƒкЅдµƒ∆µ эЈ÷≤ЉЉ∞ґ‘°∞ є”√ќҐ–≈љїЅч°±‘ё≥…»Ћ э»зѕ¬±н.
ƒкЅд£®µ•ќї£ЇЋк£© |
|
|
|
|
|
|
∆µ э | 5 | 10 | 15 | 10 | 5 | 5 |
‘ё≥…»Ћ э | 5 | 10 | 12 | 7 | 2 | 1 |
£®Ґс£©»ф“‘°∞ƒкЅд°±45Ћкќ™Ј÷љзµг£ђ”…“‘…ѕЌ≥Љ∆ эЊЁЌк≥…ѕ¬√ж ![]() Ѕ–Ѕ™±н£ђ≤Ґ≈–ґѕ «Јс”–99%µƒ∞—ќ’»ѕќ™°∞ є”√ќҐ–≈љїЅч°±µƒћђґ»”л»ЋµƒƒкЅд”–єЎ£ї
Ѕ–Ѕ™±н£ђ≤Ґ≈–ґѕ «Јс”–99%µƒ∞—ќ’»ѕќ™°∞ є”√ќҐ–≈љїЅч°±µƒћђґ»”л»ЋµƒƒкЅд”–єЎ£ї
ƒкЅд≤їµЌ”Џ45Ћкµƒ»Ћ э | ƒкЅдµЌ”Џ45Ћкµƒ»Ћ э | ЇѕЉ∆ | |
‘ё≥… | |||
≤ї‘ё≥… | |||
ЇѕЉ∆ |
£®Ґт£©»фі”ƒкЅд‘Џ ![]() ЇЌ
ЇЌ ![]() µƒ±їµч≤й»Ћ÷–∞і’’Ј÷≤г≥й—щµƒЈљЈ®—°»°6»Ћљш––„Ј„ўµч≤й£ђ≤ҐЄш”и∆д÷–3»Ћ°∞Їм∞ь°±љ±јш£ђ«у3»Ћ÷–÷Ѕ…ў”–1»ЋƒкЅд‘Џ
µƒ±їµч≤й»Ћ÷–∞і’’Ј÷≤г≥й—щµƒЈљЈ®—°»°6»Ћљш––„Ј„ўµч≤й£ђ≤ҐЄш”и∆д÷–3»Ћ°∞Їм∞ь°±љ±јш£ђ«у3»Ћ÷–÷Ѕ…ў”–1»ЋƒкЅд‘Џ ![]() µƒЄ≈¬ .
µƒЄ≈¬ .
≤ќњЉ эЊЁ»зѕ¬£Ї
ЄљЅўљз÷µ±н£Ї
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() µƒєџ≤в÷µ£Ї
µƒєџ≤в÷µ£Ї ![]() £®∆д÷–
£®∆д÷– ![]() £©
£©
°Њір∞Є°њљв£Ї£®Ґс£©ЄщЊЁћхЉюµ√ ![]() Ѕ–Ѕ™±н£Ї
Ѕ–Ѕ™±н£Ї
ƒкЅд≤їµЌ”Џ45Ћкµƒ»Ћ э | ƒкЅдµЌ”Џ45Ћкµƒ»Ћ э | ЇѕЉ∆ | |
‘ё≥… | 10 | 27 | 37 |
≤ї‘ё≥… | 10 | 3 | 13 |
Їѕ Љ∆ | 20 | 30 | 50 |
ЄщЊЁЅ–Ѕ™±нЋщЄшµƒ эЊЁіъ»лєЂ љµ√µљ£Ї ![]()
Ћщ“‘”–99%µƒ∞—ќ’»ѕќ™°∞ є”√ќҐ–≈љїЅч°±µƒћђґ»”л»ЋµƒƒкЅд”–єЎ£ї
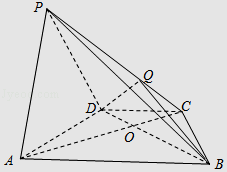
£®Ґт£©љв£Ї∞і’’Ј÷≤г≥й—щЈљЈ®њ…÷™£Ї ![]() ≥й»°£Ї
≥й»°£Ї ![]() £®»Ћ£©£ї
£®»Ћ£©£ї
![]() ≥й»°£Ї
≥й»°£Ї ![]() £®»Ћ£©
£®»Ћ£©
‘Џ…ѕ ц≥й»°µƒ6»Ћ÷–£ђƒкЅд‘Џ ![]() ”–2»Ћ£ђƒкЅд
”–2»Ћ£ђƒкЅд ![]() ”–4»Ћ£Ѓ
”–4»Ћ£Ѓ
ƒкЅд‘Џ ![]() Љ«ќ™
Љ«ќ™ ![]() £їƒкЅд‘Џ
£їƒкЅд‘Џ ![]() Љ«ќ™
Љ«ќ™ ![]() £ђ‘ті”6»Ћ÷–»ќ»°3√ыµƒЋщ”–«йњцќ™£Ї
£ђ‘ті”6»Ћ÷–»ќ»°3√ыµƒЋщ”–«йњцќ™£Ї ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ 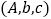 °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() є≤20÷÷«йњц£ђ
є≤20÷÷«йњц£ђ
∆д÷–÷Ѕ…ў”–“ї»ЋƒкЅд‘Џ ![]() Ћк«йњц”–£Ї
Ћк«йњц”–£Ї ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() °Ґ
°Ґ ![]() £ђє≤16÷÷«йњц£Ѓ
£ђє≤16÷÷«йњц£Ѓ
Љ«÷Ѕ…ў”–“ї»ЋƒкЅд‘Џ ![]() Ћкќ™ ¬Љю
Ћкќ™ ¬Љю ![]() £ђ‘т
£ђ‘т ![]()
°а÷Ѕ…ў”–“ї»ЋƒкЅд‘Џ ![]() Ћк÷ЃЉдµƒЄ≈¬ ќ™
Ћк÷ЃЉдµƒЄ≈¬ ќ™ ![]()
°Њљвќц°њ(1)”…ЌЉ±нњ…÷™«у≥ц—щ±ЊЈљ≤оµƒ÷µљш––ґ‘±»µ√≥цљб¬џ°£(2£©јы”√Ј÷≤г≥й—щµ√≥ц‘Џ√њЄцƒкЅдљ„ґќµƒ»Ћ эќ™6»Ћ£ђЄщЊЁћв“вЅ–Њў≥ці”6»Ћ÷–»ќ»°»э»Ћµƒ«йњц”–20÷÷£ђљбЇѕЌђ“вњ…µ√÷Ѕ…ў”–“ї»Ћ‘Џ [ 55 , 65 )µƒ«йњц”–16÷÷£ђјы”√Є≈¬ µƒґ®“е«у≥ц∆д÷µЉіњ…°£
°ЊњЉµгЊЂќц°њљвіріЋћвµƒєЎЉь‘Џ”ЏјнљвЈ÷≤г≥й—щµƒѕаєЎ÷™ ґ£ђ’∆ќ’ѕ»љЂ„№ће÷–µƒЋщ”–µ•ќї∞і’’ƒ≥÷÷ћЎ’чїт±к÷Њ£®–‘±р°ҐƒкЅдµ»£©їЃЈ÷≥…»фЄ…ја–Ќїт≤гіќ£ђ»їЇу‘ў‘ЏЄчЄцја–Ќїт≤гіќ÷–≤…”√Љтµ•Ћжїъ≥й—щїтѕµ”√≥й—щµƒ∞мЈ®≥й»°“їЄц„”—щ±Њ£ђ„оЇу£ђљЂ’в–©„”—щ±ЊЇѕ∆рјієє≥…„№ћеµƒ—щ±Њ£Ѓ

 «б«…ґбєЏ÷№≤⑬њЉ÷±Ќ®ЄяњЉѕµЅ–ір∞Є
«б«…ґбєЏ÷№≤⑬њЉ÷±Ќ®ЄяњЉѕµЅ–ір∞Є