题目内容
16.圆心为C(3,$\frac{π}{6}$),半径为3的圆的极坐标方程为ρ=6cos(θ-$\frac{π}{6}$).分析 设圆上任一点为P(ρ,θ),A(6,$\frac{π}{6}$),则OP=ρ,∠POA=θ-$\frac{π}{6}$,OA=2×3=6,Rt△OAP中,由OP=OAcos∠POA,化简可得圆的极坐标方程.
解答 解:设圆上任一点为P(ρ,θ),A(6,$\frac{π}{6}$),则OP=ρ,∠POA=θ-$\frac{π}{6}$,OA=2×3=6,
Rt△OAP中,OP=OAcos∠POA,ρ=6cos(θ-$\frac{π}{6}$),
而点O(0,$\frac{2}{3}$π),A(6,$\frac{π}{6}$) 符合,
故所求圆的极坐标方程为ρ=6cos(θ-$\frac{π}{6}$).
故答案为:ρ=6cos(θ-$\frac{π}{6}$).
点评 本题考查求圆的极坐标方程的方法,判断OP=ρ,∠POA=θ-$\frac{π}{6}$,OA=2×3=6,是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积是( )
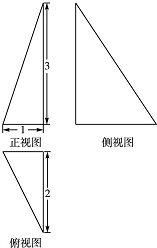

| A. | 1 m3 | B. | 2 cm3 | C. | 3 cm3 | D. | 6 cm3 |
5.目前我国很多城市出现了雾霾天气,已经给广大人民的健康带来影响,其中汽车尾气排放是造成雾霾天气的重要因素之一,很多城市提倡绿色出行方式,实施机动车尾号限行.某市为了解民众对“车辆限行”的态度,随机调查了50人,并半调查结果制成如表:
(1)若从年龄在[15,25)、[25,35)的被调查者中随机选取2人进行跟踪调查,记选中的4人中不赞成“车辆限行”的人数记为X,求X的分布列和期望;
(2)把年龄在[15,45)称为中青年,年龄在[45,75)称为中老年,请根据上表完成2×2列联表,并说明民众对“车辆限行”的态度与年龄是否有关联.
参考公式和数据:x2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(2)把年龄在[15,45)称为中青年,年龄在[45,75)称为中老年,请根据上表完成2×2列联表,并说明民众对“车辆限行”的态度与年龄是否有关联.
| 态度 年龄 | 赞成 | 不赞成 | 总计 |
| 中青年 | |||
| 中老年 | |||
| 总计 |
| X2 | ≤2.706 | >2.706 | >3.841 | >6.635 |
| A、B关联性 | 无关联 | 90% | 95% | 99% |
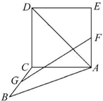 如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$. 为了解沈阳市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
为了解沈阳市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.