题目内容
1.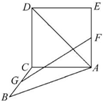 如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
分析 以C为原点,CB为x轴,CA为y轴,CD为z轴,建立空间直角坐标系,利用向量法能求出AD与GF所成的角的余弦值.
解答 解:如图,以C为原点,CB为x轴,CA为y轴,CD为z轴,建立空间直角坐标系,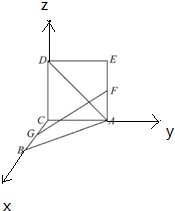
由已知得A(0,2,0),D(0,0,2),G(1,0,0),F(0,2,1),
$\overrightarrow{AD}$=(0,-2,2),$\overrightarrow{GF}$=(-1,2,1),
设AD与GF所成的角为θ,
则cosθ=|cos<$\overrightarrow{AD},\overrightarrow{GF}$>|=|$\frac{\overrightarrow{AD}•\overrightarrow{GF}}{|\overrightarrow{AD}|•|\overrightarrow{GF}|}$|=|$\frac{0-4+2}{\sqrt{8}•\sqrt{6}}$|=$\frac{\sqrt{3}}{6}$.
故答案为:$\frac{\sqrt{3}}{6}$.
点评 本题考查异面直线所成角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
6.把函数y=cos(2x+φ)(|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{6}$个单位,得到函数y=f(x)的图象关于直线x=$\frac{5π}{12}$对称,则φ的值为( )
| A. | -$\frac{π}{12}$ | B. | -$\frac{π}{6}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
11.已知x,y的取值如表所示:
从散点图可以看出,y与x线性相关,若回归方程为$\widehat{y}$=1.46x+a,则实数a=-0.61.
| x | 2 | 3 | 4 | 5 |
| y | 2.2 | 3.8 | 5.5 | 6.5 |