题目内容
如图,已知矩形ABCD中,AB=1,BC=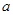
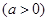 ,PA
,PA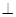 平面ABCD,且PA=1。
平面ABCD,且PA=1。
(1)问BC边上是否存在点Q,使得PQ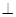 QD?并说明理由;
QD?并说明理由;
(2)若边上有且只有一个点Q,使得PQ QD,求这时二面角Q
QD,求这时二面角Q 的正切。
的正切。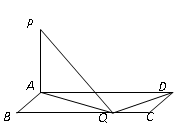
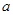
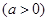 ,PA
,PA 平面ABCD,且PA=1。
平面ABCD,且PA=1。(1)问BC边上是否存在点Q,使得PQ
 QD?并说明理由;
QD?并说明理由;(2)若边上有且只有一个点Q,使得PQ
 QD,求这时二面角Q
QD,求这时二面角Q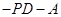 的正切。
的正切。
(1) (i)当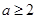 时,BC上存在点Q,使PQ
时,BC上存在点Q,使PQ QD;
QD;
(ii)当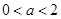 时,BC上不存在点Q,使PQ
时,BC上不存在点Q,使PQ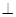 QD。
QD。
(2)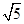
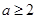 时,BC上存在点Q,使PQ
时,BC上存在点Q,使PQ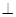 QD;
QD;(ii)当
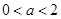 时,BC上不存在点Q,使PQ
时,BC上不存在点Q,使PQ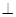 QD。
QD。(2)
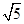
(1)(如图)以A为原点建立空间直角坐标系,设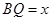 ,
,
则Q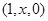 ,P(0,0,1),D
,P(0,0,1),D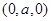 得
得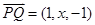 ,
,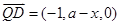
由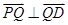 ,有
,有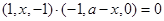 ,得
,得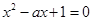 ①
①
若方程①有解,必为正数解,且小于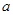 。
。
由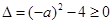 ,
,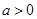 ,得
,得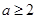 。
。
(i)当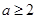 时,BC上存在点Q,使PQ
时,BC上存在点Q,使PQ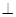 QD;
QD;
(ii)当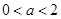 时,BC上不存在点Q,使PQ
时,BC上不存在点Q,使PQ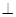 QD。
QD。
(2)要使BC边上有且只有一个点Q,使PQ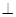 QD,则方程①有两个相等的实根,
QD,则方程①有两个相等的实根,
这时,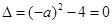 ,得
,得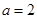 ,有
,有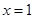 。
。
又平面APD的法向量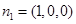 ,设平面PQD的法向量为
,设平面PQD的法向量为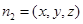
而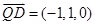 ,
,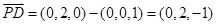 ,
,
由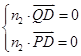 ,得
,得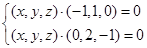 ,解得
,解得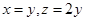
有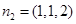 ,则
,则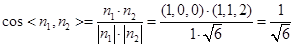 ,则
,则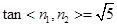 。
。
所以二面角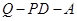 的正切为
的正切为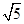
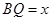 ,
,则Q
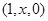 ,P(0,0,1),D
,P(0,0,1),D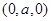 得
得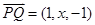 ,
,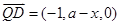
由
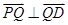 ,有
,有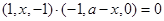 ,得
,得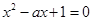 ①
①若方程①有解,必为正数解,且小于
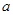 。
。由
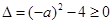 ,
,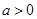 ,得
,得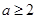 。
。(i)当
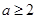 时,BC上存在点Q,使PQ
时,BC上存在点Q,使PQ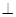 QD;
QD;(ii)当
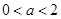 时,BC上不存在点Q,使PQ
时,BC上不存在点Q,使PQ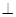 QD。
QD。(2)要使BC边上有且只有一个点Q,使PQ
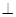 QD,则方程①有两个相等的实根,
QD,则方程①有两个相等的实根,这时,
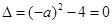 ,得
,得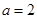 ,有
,有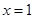 。
。又平面APD的法向量
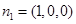 ,设平面PQD的法向量为
,设平面PQD的法向量为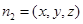
而
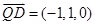 ,
,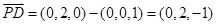 ,
,由
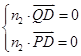 ,得
,得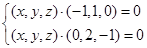 ,解得
,解得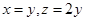
有
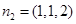 ,则
,则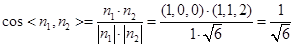 ,则
,则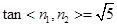 。
。所以二面角
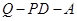 的正切为
的正切为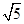

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.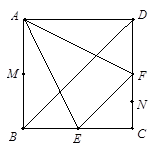
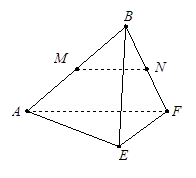
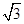 ,VC=7,画出二面角V-AB-C的平面角,并求它的余弦值。
,VC=7,画出二面角V-AB-C的平面角,并求它的余弦值。 中,二面角
中,二面角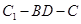 的正切值为 ___.
的正切值为 ___.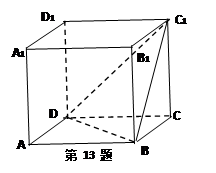
 中,若点
中,若点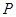 是棱上一点,则满足
是棱上一点,则满足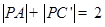 的点
的点
 为多面体,平面
为多面体,平面 与平面
与平面 垂直,点
垂直,点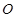 在线段
在线段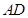 上,
上,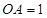 ,
,
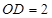 ,△OAB,△OAC,△ODE,△ODF都是正三角形。
,△OAB,△OAC,△ODE,△ODF都是正三角形。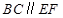 ;
;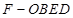 的体积.
的体积.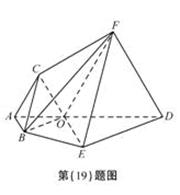
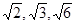 ,这个长方体对角线的长是 .
,这个长方体对角线的长是 .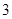 ,圆心角为
,圆心角为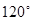 的扇形,则圆锥的底面圆半径是
的扇形,则圆锥的底面圆半径是