题目内容
如图,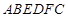 为多面体,平面
为多面体,平面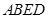 与平面
与平面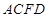 垂直,点
垂直,点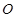 在线段
在线段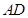 上,
上,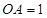 ,
,
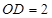 ,△OAB,△OAC,△ODE,△ODF都是正三角形。
,△OAB,△OAC,△ODE,△ODF都是正三角形。
(Ⅰ)证明直线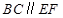 ;
;
(Ⅱ)求棱锥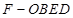 的体积.
的体积.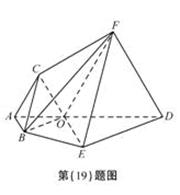
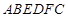 为多面体,平面
为多面体,平面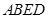 与平面
与平面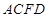 垂直,点
垂直,点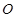 在线段
在线段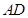 上,
上,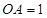 ,
,
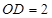 ,△OAB,△OAC,△ODE,△ODF都是正三角形。
,△OAB,△OAC,△ODE,△ODF都是正三角形。(Ⅰ)证明直线
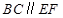 ;
;(Ⅱ)求棱锥
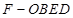 的体积.
的体积.
(I)证明:设G是线段DA与EB延长线的交点. 由于△OAB与△ODE都是正三角形,所以
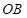 ∥
∥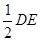 ,OG=OD=2,同理,设
,OG=OD=2,同理,设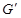 是线段DA与FC延长线的交点,有
是线段DA与FC延长线的交点,有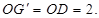 又由于G和
又由于G和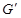 都在线段DA的延长线上,所以G与
都在线段DA的延长线上,所以G与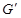 重合.
重合.
在△GED和△GFD中,由
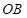 ∥
∥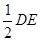 和OC∥
和OC∥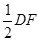 ,可知B和C分别是GE和GF的中点,所以BC是△GEF的中位线,故BC∥EF.(II)解:由OB=1,OE=2,
,可知B和C分别是GE和GF的中点,所以BC是△GEF的中位线,故BC∥EF.(II)解:由OB=1,OE=2,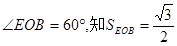 ,而△OED是边长为2的正三角形,故
,而△OED是边长为2的正三角形,故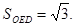 所以
所以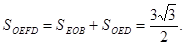
过点F作FQ⊥DG,交DG于点Q,由平面ABED⊥平面ACFD知,FQ就是四棱锥F—OBED的高,且FQ=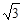 ,所以
,所以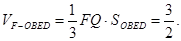
|
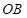 ∥
∥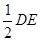 ,OG=OD=2,同理,设
,OG=OD=2,同理,设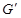 是线段DA与FC延长线的交点,有
是线段DA与FC延长线的交点,有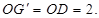 又由于G和
又由于G和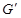 都在线段DA的延长线上,所以G与
都在线段DA的延长线上,所以G与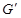 重合.
重合.
|
|
|
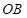 ∥
∥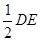 和OC∥
和OC∥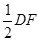 ,可知B和C分别是GE和GF的中点,所以BC是△GEF的中位线,故BC∥EF.(II)解:由OB=1,OE=2,
,可知B和C分别是GE和GF的中点,所以BC是△GEF的中位线,故BC∥EF.(II)解:由OB=1,OE=2,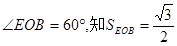 ,而△OED是边长为2的正三角形,故
,而△OED是边长为2的正三角形,故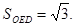 所以
所以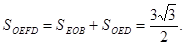
过点F作FQ⊥DG,交DG于点Q,由平面ABED⊥平面ACFD知,FQ就是四棱锥F—OBED的高,且FQ=
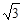 ,所以
,所以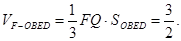
略

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
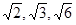 ,这个长方体它的八个顶点都在同一个球面上,这个球的表面积是( )
,这个长方体它的八个顶点都在同一个球面上,这个球的表面积是( )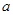
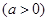 ,PA
,PA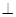 平面ABCD,且PA=1。
平面ABCD,且PA=1。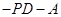 的正切。
的正切。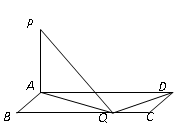
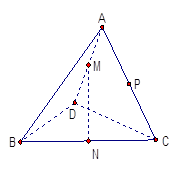
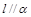 ,
,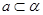 ,则
,则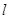 与
与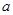 的位置关系一定是( )
的位置关系一定是( )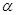 没有公共点
没有公共点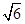 ,AD=2,则A、D两点间的球面距离为
,AD=2,则A、D两点间的球面距离为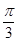 B、
B、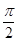 C、
C、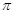 D、
D、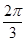
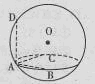
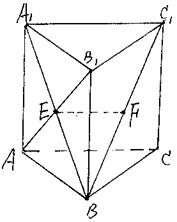
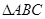 是等腰直角三角形,
是等腰直角三角形,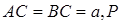 是
是 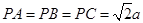
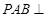 面
面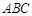 ;
;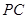 和
和
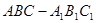 中,
中,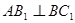 ,
,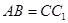
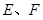 分别为
分别为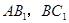 的中点
的中点

 、
、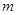 ,两个不重合的平面α、β,
,两个不重合的平面α、β,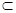 β,给出下列命题:①α∥β
β,给出下列命题:①α∥β