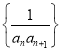题目内容
【题目】已知函数![]() .
.
(1)若![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)求出![]() ,分两种情况讨论
,分两种情况讨论![]() 的范围,分别令
的范围,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)分三种情况讨论
的减区间;(2)分三种情况讨论![]() 的范围,函数
的范围,函数![]() 在
在![]() 上恒成立,当
上恒成立,当![]() 时,等价于
时,等价于![]() ;当
;当![]() 时,等价于
时,等价于![]() ,分别利用导数研究函数的单调性,求出函数的最值,可得结果.
,分别利用导数研究函数的单调性,求出函数的最值,可得结果.
(1)依题意, ![]() ,
,
若![]() ,则函数
,则函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
若![]() ,则函数
,则函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
(2)因为![]() ,故
,故![]() ,①
,①
当![]() 时,显然①不成立;
时,显然①不成立;
当![]() 时,①化为:
时,①化为: ![]() ;②
;②
当![]() 时,①化为:
时,①化为: ![]() ;③
;③
当![]() 时,①化为:
时,①化为: ![]() ;③
;③
令![]() ,则
,则![]() ,
,
![]() 当
当![]() 时,
时, ![]() 时,
时, ![]() ,
,
故![]() 在
在![]() 是增函数,在
是增函数,在![]() 是减函数,
是减函数, ![]() ,
,
因此②不成立,要③成立,只要![]() ,
,
![]() 所求
所求![]() 的取值范围是
的取值范围是![]() .
.
【方法点晴】本题主要考查利用导数研究函数的单调性、利用导数求函数的最值以及不等式恒成立问题,属于难题.不等式恒成立问题常见方法:① 分离参数![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 数形结合(
即可);② 数形结合(![]() 图象在
图象在![]() 上方即可);③ 讨论最值
上方即可);③ 讨论最值![]() 或
或![]() 恒成立;④ 讨论参数.
恒成立;④ 讨论参数.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案【题目】某地![]() 户家庭的年收入
户家庭的年收入![]() (万元)和年饮食支出
(万元)和年饮食支出![]() (万元)的统计资料如下表:
(万元)的统计资料如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;(结果保留到小数点后
的线性回归方程;(结果保留到小数点后![]() 为数字)
为数字)
(2)利用(1)中的回归方程,分析这![]() 户家庭的年饮食支出的变化情况,并预测该地年收入
户家庭的年饮食支出的变化情况,并预测该地年收入![]() 万元的家庭的年饮食支出.(结果保留到小数点后
万元的家庭的年饮食支出.(结果保留到小数点后![]() 位数字)
位数字)
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
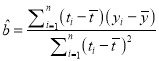 ,
, ![]()
【题目】微信是当前主要的社交应用之一,有着几亿用户,覆盖范围广,及时快捷,作为移动支付的重要形式,微信支付成为人们支付的重要方式和手段。某公司为了解人们对“微信支付”认可度,对![]() 年龄段的人群随机抽取
年龄段的人群随机抽取![]() 人进行了一次“你是否喜欢微信支付”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次“你是否喜欢微信支付”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
组号 | 分组 | 喜欢微信支付的人数 | 喜欢微信支付的人数 占本组的频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
第六组 |
|
|
|

(1)补全频率分布直方图,并求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)在第四、五、六组“喜欢微信支付”的人中,用分层抽样的方法抽取![]() 人参加“微信支付日鼓励金”活动,求第四、五、六组应分别抽取的人数;
人参加“微信支付日鼓励金”活动,求第四、五、六组应分别抽取的人数;
(3)在(2)中抽取的![]() 人中随机选派
人中随机选派![]() 人做采访嘉宾,求所选派的
人做采访嘉宾,求所选派的![]() 人没有第四组人的概率.
人没有第四组人的概率.
【题目】某城市为鼓励人们绿色出行,乘坐地铁,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过![]() 站的地铁票价如下表:
站的地铁票价如下表:
乘坐站数 |
|
|
|
票价(元) |
|
|
|
现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过![]() 站.甲、乙乘坐不超过
站.甲、乙乘坐不超过![]() 站的概率分别为
站的概率分别为![]() ,
, ![]() ;甲、乙乘坐超过
;甲、乙乘坐超过![]() 站的概率分别为
站的概率分别为![]() ,
, ![]() .
.
(1)求甲、乙两人付费相同的概率;
(2)设甲、乙两人所付费用之和为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.