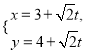题目内容
【题目】已知函数![]() ,
, ![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求函数![]() 的单调区间与极值;
的单调区间与极值;
(2)若存在实数![]() ,使得
,使得![]() 成立,求整数
成立,求整数![]() 的最小值.
的最小值.
【答案】(1) 函数f(x)的单调递减区间为(-∞,0);单调递增区间为(0,+∞),所以函数f(x)在x=0处取得极小值f(0)=2;(2) k的最小值为0.
【解析】试题分析:⑴求出函数![]() 的导数,求得切线的切点,
的导数,求得切线的切点,
⑵要满足![]() ,分类含参量得
,分类含参量得![]()
构造![]() ,求得
,求得![]() 的最小值即可
的最小值即可
解析:(Ⅰ)f′(x)=2ex+6x-2,
因为f′(0)=a,所以a=0,
易得切点(0,2),所以b=-1.
易知函数f′(x)在R上单调递增,且f′(0)=0.
则当x<0时,f′(x)<0;当x>0时,f′(x)>0.
所以函数f(x)的单调递减区间为(-∞,0);单调递增区间为(0,+∞).
所以函数f(x)在x=0处取得极小值f(0)=2.
(Ⅱ)f(x)-2x2-3x-2-2k≤0![]() ex+
ex+![]() x2-
x2-![]() x-1-k≤0
x-1-k≤0![]() k≥ex+
k≥ex+![]() x2-
x2-![]() x-1, (*)
x-1, (*)
令h(x)=ex+![]() x2-
x2-![]() x-1,
x-1,
若存在实数x,使得不等式(*)成立,则k≥h(x)min,
h′(x)=ex+x-![]() ,易知h′(x)在R上单调递增,
,易知h′(x)在R上单调递增,
又h′(0)=-![]() <0,h′(1)=e-
<0,h′(1)=e-![]() >0,h′
>0,h′![]() =e
=e![]() -2<0,h′
-2<0,h′![]() =e
=e![]() -
-![]() >2.56
>2.56![]() -
-![]() =1.6
=1.6![]() -
-![]() =
=![]() -
-![]() >2-
>2-![]() =
=![]() >0,
>0,
![]()
![]()
所以存在唯一的x0∈![]() ,使得h′(x0)=0,
,使得h′(x0)=0,
且当x∈(-∞,x0)时,h′(x)<0;当x∈(x0,+∞)时,h′(x)>0.
所以h(x)在(-∞,x0)上单调递减,在(x0,+∞)上单调递增,
h(x)min=h(x0)=ex0+![]() x20-
x20-![]() x0-1,
x0-1,
又h′(x0)=0,即ex0+x0-![]() =0,
=0,
所以ex0=![]() -x0.
-x0.
所以![]()
![]()
因为x0∈![]() ,
,
所以h(x0)∈![]() ,
,
则k≥h(x0),又k∈Z.
所以k的最小值为0.

【题目】现在的人基本每天都离不开手机,许多人手机一旦不在身边就不舒服,几乎达到手机二十四小时不离身,这类人群被称为“手机控”,这一群体在大学生中比较突出.为了调查大学生每天使用手机的时间,某调查公司针对某高校男生、女生各25名学生进行了调查,其中每天使用手机时间超过8小时的被称为:“手机控”,否则被称为“非手机控”.调查结果如下:
手机控 | 非手机控 | 合计 | |
女生 | 5 | ||
男生 | 10 | ||
合计 | 50 |
(1)将上面的列联表补充完整,再判断是否有99.5%的把握认为“手机控”与性别有关,说明你的理由;
(2)现从被调查的男生中按分层抽样的方法选出5人,再从这5人中随机选取3人参加座谈会,记这3人中“手机控”的人数为![]() ,试求
,试求![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式: 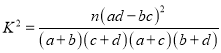 ,其中
,其中![]() .
.