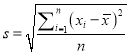��Ŀ����
����Ŀ�����ǵ�ǰ��Ҫ���罻Ӧ��֮һ�����ż����û������Ƿ�Χ�㣬��ʱ��ݣ���Ϊ�ƶ�֧������Ҫ��ʽ����֧����Ϊ����֧������Ҫ��ʽ���ֶΡ�ij��˾Ϊ�˽����Ƕԡ���֧�����Ͽɶȣ���![]() ����ε���Ⱥ�����ȡ
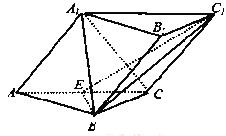
����ε���Ⱥ�����ȡ![]() �˽�����һ�Ρ����Ƿ�ϲ����֧�������ʾ����飬���ݵ������õ�����ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
�˽�����һ�Ρ����Ƿ�ϲ����֧�������ʾ����飬���ݵ������õ�����ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
��� | ���� | ϲ����֧�������� | ϲ����֧�������� ռ�����Ƶ�� |
��һ�� |
|
|
|
�ڶ��� |
|
|
|
������ |
|
|
|
������ |
|
|
|
������ |
|
|
|
������ |
|
|
|

��1����ȫƵ�ʷֲ�ֱ��ͼ������![]() ��
�� ![]() ��
�� ![]() ��ֵ��
��ֵ��
��2���ڵ��ġ��塢���顰ϲ����֧���������У��÷ֲ�����ķ�����ȡ![]() �˲μӡ���֧���չ��������������ġ��塢����Ӧ�ֱ��ȡ��������
�˲μӡ���֧���չ��������������ġ��塢����Ӧ�ֱ��ȡ��������
��3���ڣ�2���г�ȡ��![]() �������ѡ��
�������ѡ��![]() �����ɷüα�������ѡ�ɵ�
�����ɷüα�������ѡ�ɵ�![]() ��û�е������˵ĸ���.
��û�е������˵ĸ���.
���𰸡�(1) ![]() ,
,![]() ,
,![]() ����2��
����2��![]() ��(3)
��(3) ![]() .
.
�������������������1����Ƶ�ʱ��е��������ݿ�֪��������������Ϊ![]() ���ٽ��Ƶ�ʷֲ�ֱ��ͼ��
���ٽ��Ƶ�ʷֲ�ֱ��ͼ��
�������![]() ��ֵ��
��ֵ��
��2����Ϊ���ġ��塢���顰ϲ����֧��������������![]() �ˣ��ɷֲ����ԭ����֪�����ġ��塢����ֱ�ȡ��������
�ˣ��ɷֲ����ԭ����֪�����ġ��塢����ֱ�ȡ��������
��3���������4����![]() ��������2����
��������2����![]() ��������1����
��������1����![]() ��
��
�г���7���������ȡ2�����п��ܵĽ�������ùŵ���ͼ�����ʵĸ��ʵļ��㹫ʽ����
����������
���������
��1����ͼ,��Ƶ�ʱ��е��������ݿ�֪��������������Ϊ![]() ���ٽ��Ƶ�ʷֲ�ֱ��ͼ
���ٽ��Ƶ�ʷֲ�ֱ��ͼ
��֪![]()
����![]()
�ڶ����Ƶ��Ϊ![]() ������
������![]()
��2����Ϊ���ġ��塢���顰ϲ����֧��������������105�ˣ��ɷֲ����ԭ����֪�����ġ��塢����ֱ�ȡ������Ϊ4�ˣ�2�ˣ�1��.
��3���������4����![]() ��������2����
��������2����![]() ��������1����
��������1����![]() .
.
���7���������ȡ2�����п��ܵĽ��Ϊ��
![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� 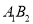 ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]()
![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��21�֣�
��21�֣�
����ǡ��û�е������˵����п��ܽ��Ϊ��![]() ����3�֣�
����3�֣�
��������ȡ��2����ǡ��û�е������˵ĸ���Ϊ![]() .
.

����Ŀ���߿���ϰ�������֡�����ʶ�㡱֮��Ϊ���о���ǰ����ʱ���֡�ǿ��ѵ������![]() �������ȷ��
�������ȷ��![]() �Ĺ�ϵ����ijУ����ij��ѧ�������˹�עͳ�ƣ��õ�������ݣ�
�Ĺ�ϵ����ijУ����ij��ѧ�������˹�עͳ�ƣ��õ�������ݣ�
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
��1����![]() ����
����![]() �����Իع鷽�̣���Ԥ�������ȷ����
�����Իع鷽�̣���Ԥ�������ȷ����![]() ��ǿ��ѵ��������������������
��ǿ��ѵ��������������������
��2������![]() ��
��![]() ����ʾͳ�����ݵġ�ǿ����ֵ��������������������ǿ����ֵ���ı���������
����ʾͳ�����ݵġ�ǿ����ֵ��������������������ǿ����ֵ���ı���������![]() �ڣ���ǿ��ѵ����Ч������������ǿ��ѵ���Ƿ���Ч��
�ڣ���ǿ��ѵ����Ч������������ǿ��ѵ���Ƿ���Ч��
�����ع�ֱ�ߵ�б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��
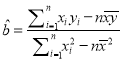 ��
�� ![]() ����������
����������![]() ��
�� ![]() ������
������ ![]() �ı���Ϊ
�ı���Ϊ