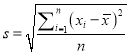题目内容
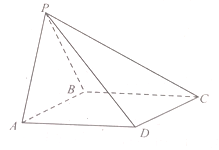
【题目】如图,已知四棱锥![]() ,
, ![]() 平面
平面![]() ,底面
,底面![]() 中,
中, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)问在棱![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ,若存在,请求出二面角
,若存在,请求出二面角![]() 的余弦值;若不存在,请说明理由.
的余弦值;若不存在,请说明理由.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)要证平面![]() 平面
平面![]() ,即证
,即证![]() 平面
平面![]() ,即证:
,即证: ![]()
(2) 存在点![]() 使
使![]() 平面
平面![]() ,在
,在![]() 内,过
内,过![]() 做
做![]() 垂足为
垂足为![]() ,易知
,易知![]() 为二面角
为二面角![]() 的平面角,从而得到结果.
的平面角,从而得到结果.
试题解析:
方法一:(1)证明:∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() . ∵
. ∵![]() 为
为![]() 的中点,且梯形
的中点,且梯形![]() 中
中![]() ,
, ![]() ,
,
∴![]()
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,且
,且![]()
∴![]() 平面
平面![]() .
.
![]() 平面
平面![]() , ∴平面
, ∴平面![]() ⊥平面
⊥平面![]()
(2)存在点![]() 使
使![]() 平面
平面![]() ,在
,在![]() 内,过
内,过![]() 做
做![]() 垂足为
垂足为![]()
由(1)![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
,
![]() ,
, ![]() 平面
平面![]()
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() 知
知 ![]() ,
, ![]()
∵平面![]() 平面
平面![]()
∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
故二面角![]() 的余弦值为
的余弦值为![]() .
.
方法二:
∴以![]() 为原点,射线
为原点,射线![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 轴的正半轴,建立空间直角坐标系如图
轴的正半轴,建立空间直角坐标系如图
![]() ,
,
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
, ![]()
(1)![]()
∴![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,且
,且![]()
∴![]() 平面
平面![]() .
.
![]() 平面
平面![]() , ∴平面
, ∴平面![]() ⊥平面
⊥平面![]()
(2)存在点![]() 使
使![]() 平面
平面![]() ,在
,在![]() 内,过
内,过![]() 做
做![]() 垂足为
垂足为![]()
由(1)![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
,

![]() ,
, ![]() 平面
平面![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() ,
,
![]() ,
,
取![]() .
.
![]()
![]() 平面
平面![]()
![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
由图形知二面角![]() 的平面角
的平面角![]() 是锐角,
是锐角,
故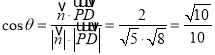
所以二面角余弦值为![]()

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案【题目】现在的人基本每天都离不开手机,许多人手机一旦不在身边就不舒服,几乎达到手机二十四小时不离身,这类人群被称为“手机控”,这一群体在大学生中比较突出.为了调查大学生每天使用手机的时间,某调查公司针对某高校男生、女生各25名学生进行了调查,其中每天使用手机时间超过8小时的被称为:“手机控”,否则被称为“非手机控”.调查结果如下:
手机控 | 非手机控 | 合计 | |
女生 | 5 | ||
男生 | 10 | ||
合计 | 50 |
(1)将上面的列联表补充完整,再判断是否有99.5%的把握认为“手机控”与性别有关,说明你的理由;
(2)现从被调查的男生中按分层抽样的方法选出5人,再从这5人中随机选取3人参加座谈会,记这3人中“手机控”的人数为![]() ,试求
,试求![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式: 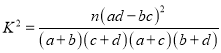 ,其中
,其中![]() .
.
【题目】高考复习经过二轮“见多识广”之后,为了研究考前“限时抢分”强化训练次数![]() 与答题正确率
与答题正确率![]() 的关系,对某校高三某班学生进行了关注统计,得到如表数据:
的关系,对某校高三某班学生进行了关注统计,得到如表数据:
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
(1)求![]() 关于
关于![]() 的线性回归方程,并预测答题正确率是
的线性回归方程,并预测答题正确率是![]() 的强化训练次数(保留整数);
的强化训练次数(保留整数);
(2)若用![]() (
(![]() )表示统计数据的“强化均值”(保留整数),若“强化均值”的标准差在区间
)表示统计数据的“强化均值”(保留整数),若“强化均值”的标准差在区间![]() 内,则强化训练有效,请问这个班的强化训练是否有效?
内,则强化训练有效,请问这个班的强化训练是否有效?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
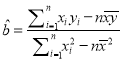 ,
, ![]() ,样本数据
,样本数据![]() ,
, ![]() ,…,
,…, ![]() 的标准差为
的标准差为