题目内容
设数列{an}前n项和为Sn,点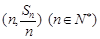 均在直线
均在直线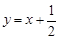 上.
上.
(1)求数列{an}的通项公式;
(2)设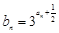 ,Tn是数列{bn}的前n项和,试求Tn;
,Tn是数列{bn}的前n项和,试求Tn;
(3)设cn=anbn,Rn是数列{cn}的前n项和,试求Rn.
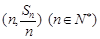 均在直线
均在直线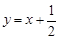 上.
上. (1)求数列{an}的通项公式;
(2)设
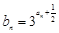 ,Tn是数列{bn}的前n项和,试求Tn;
,Tn是数列{bn}的前n项和,试求Tn;(3)设cn=anbn,Rn是数列{cn}的前n项和,试求Rn.
(1)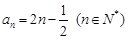 (2)
(2)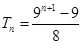 (3)
(3)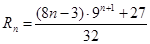
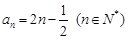 (2)
(2)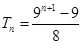 (3)
(3)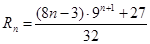
试题分析:(1)将点代入直线方程整理可得
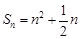 ,用公式
,用公式 可推导出
可推导出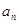 。(2)由
。(2)由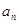 可得
可得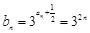 ,可证得数列
,可证得数列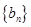 为等比数列 ,用等比数列的前
为等比数列 ,用等比数列的前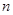 项和公式可求其前
项和公式可求其前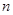 项和
项和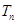 。(3)因为
。(3)因为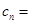 等差
等差 等比,所以用错位相减法求数列
等比,所以用错位相减法求数列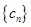 的前
的前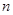 项和。
项和。试题解析:(1)依题意得,
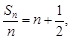 即
即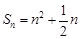 . (1分)
. (1分)当
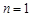 时,
时,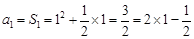 . (2分)
. (2分)当
 时,
时, 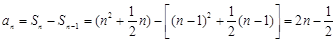 ; (4分)
; (4分)所以
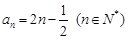 . (5分)
. (5分)(2)由(1)得
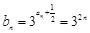 , (6分)
, (6分)由
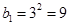 , (7分)
, (7分)由
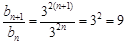 ,可知{bn}为首项为9,公比为9的等比数列. (8分)
,可知{bn}为首项为9,公比为9的等比数列. (8分)故
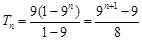 . (9分)
. (9分)(3)由(1)、(2)得
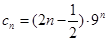 (10分)
(10分) 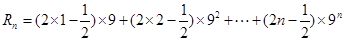 (11分)
(11分)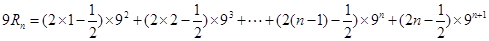 (12分)
(12分)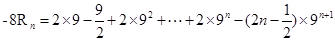 (13分)
(13分)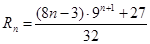 (14分)
(14分)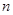 项和;4错位相减法求数列的前
项和;4错位相减法求数列的前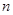 项和。
项和。
练习册系列答案
相关题目
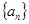 满足前
满足前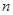 项和
项和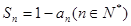 .
.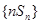 的前
的前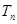 .
. an+
an+ ,则{an}的通项公式是an=________.
,则{an}的通项公式是an=________. ,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为________.
,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为________.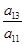 =________.
=________. B.-
B.-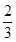 的等比数列{an}的前n项和为Sn,则 ( ).
的等比数列{an}的前n项和为Sn,则 ( ).