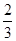题目内容
若数列{an}的前n项和Sn＝
an＋
，则{an}的通项公式是an＝________.
an＋，则{an}的通项公式是an＝________.(－2)n－1
当n＝1时，S1＝a1＋，∴a1＝1.
当n≥2时，an＝Sn－Sn－1＝an＋－
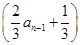＝ (an－an－1)，
∴an＝－2an－1，即
＝－2，
∴{an}是以1为首项的等比数列，其公比为－2，
∴an＝1×(－2)n－1，即an＝(－2)n－1.
a1＋，∴a1＝1.当n≥2时，an＝Sn－Sn－1＝
an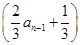＋－＝ (an－an－1)，∴an＝－2an－1，即
＝－2，∴{an}是以1为首项的等比数列，其公比为－2，
∴an＝1×(－2)n－1，即an＝(－2)n－1.
练习册系列答案
口算能手系列答案
相关题目
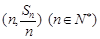均在直线
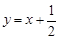上.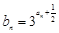 
，Tn是数列{bn}的前n项和，试求Tn;
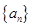的前
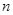项和为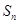
,则下列一定成立的是( )
,则
,则
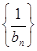的前n项和Tn.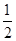
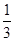
等于( )
