题目内容
设数列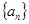 满足前
满足前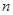 项和
项和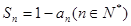 .
.
(1)求数列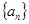 的通项公式;
的通项公式;
(2)求数列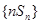 的前
的前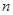 项和
项和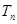 .
.
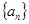 满足前
满足前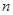 项和
项和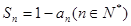 .
.(1)求数列
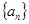 的通项公式;
的通项公式;(2)求数列
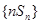 的前
的前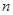 项和
项和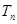 .
.(1)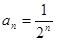 ;(2)
;(2)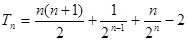 .
.
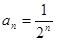 ;(2)
;(2)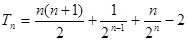 .
.试题分析:(1)由于数列的和与通项在一个等式中,通过递推一个式子即可得到关于通项的等式,从而发现是一个等比数列,但一定要验证第一项的结果是否符合;(2)由(1)可得
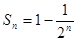 ,从而
,从而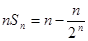 ,采用分组求和法:
,采用分组求和法: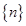 是等差数列,用等差数列的求和公式进行计算,而
是等差数列,用等差数列的求和公式进行计算,而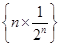 是一个等差与一个等比的乘积,故采用错位相减法求和,最后两个和之差即可得到数列
是一个等差与一个等比的乘积,故采用错位相减法求和,最后两个和之差即可得到数列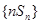 的前
的前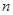 项和.
项和.试题解析:(1)当
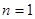 时,
时,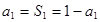 ,所以
,所以 1分
1分当
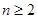 时,由
时,由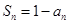 知
知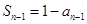
所以
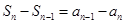 即
即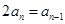 ,也就是
,也就是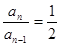 3分
3分所以数列
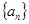 的通项公式为
的通项公式为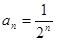 5分
5分(2)由(1)可知
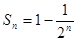 ,所以
,所以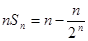 6分
6分则数列
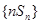 的前
的前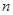 项和
项和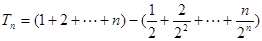
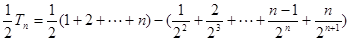 8分
8分两式相减,得
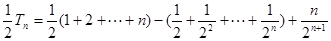
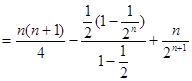 11分
11分所以数列
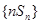 的前
的前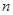 项和
项和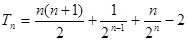 12分.
12分.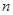 项和的计算.
项和的计算.
练习册系列答案
相关题目
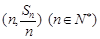 均在直线
均在直线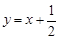 上.
上. 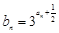 ,Tn是数列{bn}的前n项和,试求Tn;
,Tn是数列{bn}的前n项和,试求Tn;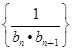 的前n项和, 求T2 013的值.
的前n项和, 求T2 013的值.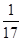
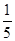
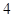 年计算机的价格降低
年计算机的价格降低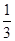 ,则
,则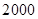 年价格为
年价格为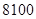 元的计算机到
元的计算机到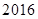 年价格应为( )
年价格应为( ) 元
元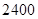 元
元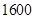 元
元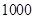 元
元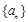 的前
的前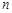 项和为
项和为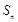 ,若
,若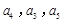 成等差数列,且
成等差数列,且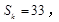
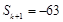 ,其中
,其中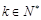 ,则
,则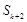 的值为 .
的值为 .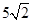
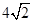
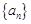 为等比数列,
为等比数列,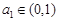 ,
,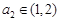 ,
,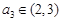 ,则
,则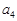 的取值范围是( )
的取值范围是( )

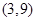

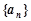 的前
的前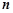 项和为
项和为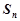 ,若
,若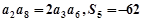 ,则
,则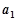 的值是 .
的值是 .