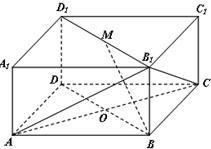
题目内容
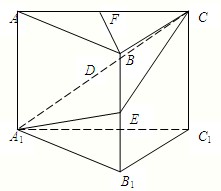
如图所示的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,O为AC与BD的交点,BB1=
,M是线段B1D1的中点.
(1)求证:BM∥平面D1AC;
(2)求三棱锥D1-AB1C的体积.
| 2 |
(1)求证:BM∥平面D1AC;
(2)求三棱锥D1-AB1C的体积.

(Ⅰ)连接D1O,如图,
∵O、M分别是BD、B1D1的中点,BD1D1B是矩形,
∴四边形D1OBM是平行四边形,
∴D1O∥BM.(2分)
∵D1O?平面D1AC,BM?平面D1AC,∴BM∥平面D1AC.(4分)
(Ⅱ)连接OB1,∵正方形ABCD的边长为2,BB1=
,
∴B1D1=2
,OB1=2,D1O=2,
则OB12+D1O2=B1D12,∴OB1⊥D1O.(6分)
又∵在长方体ABCD-A1B1C1D1中,AC⊥BD,AC⊥D1D,且BD∩D1D=D,
∴AC⊥平面BDD1B1,又D1O?平面BDD1B1,
∴AC⊥D1O,又AC∩OB1=O,(10分)
∴D1O⊥平面AB1C,即D1O为三棱锥D1-AB1C的高.(12分)
∵S△AB1C=
•AC•OB1=
×2
×2=2
,D1O=2
∴VD1-AB1C=
•S△AB1C•D1O=
×2
×2=
.14(5分)
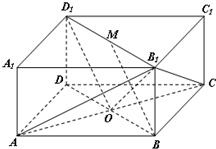
∵O、M分别是BD、B1D1的中点,BD1D1B是矩形,
∴四边形D1OBM是平行四边形,
∴D1O∥BM.(2分)
∵D1O?平面D1AC,BM?平面D1AC,∴BM∥平面D1AC.(4分)
(Ⅱ)连接OB1,∵正方形ABCD的边长为2,BB1=
| 2 |
∴B1D1=2
| 2 |
则OB12+D1O2=B1D12,∴OB1⊥D1O.(6分)
又∵在长方体ABCD-A1B1C1D1中,AC⊥BD,AC⊥D1D,且BD∩D1D=D,
∴AC⊥平面BDD1B1,又D1O?平面BDD1B1,
∴AC⊥D1O,又AC∩OB1=O,(10分)
∴D1O⊥平面AB1C,即D1O为三棱锥D1-AB1C的高.(12分)
∵S△AB1C=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∴VD1-AB1C=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目