题目内容
在体积为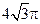 的球的表面上有A,B,C三点,AB=1,BC=
的球的表面上有A,B,C三点,AB=1,BC=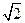 ,A,C两点的球面距离为
,A,C两点的球面距离为 ,则球心到平面ABC的距离为_________.
,则球心到平面ABC的距离为_________.
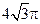 的球的表面上有A,B,C三点,AB=1,BC=
的球的表面上有A,B,C三点,AB=1,BC=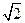 ,A,C两点的球面距离为
,A,C两点的球面距离为 ,则球心到平面ABC的距离为_________.
,则球心到平面ABC的距离为_________.: 

: 由卷头提供的公式可得球的半径为 ,由A,C两点的球面距离为
,由A,C两点的球面距离为 ,可得∠AOC=60
,可得∠AOC=60 ,AC=
,AC= ,显然△ABC是直角三角形,球心O到直角边AC的距离
,显然△ABC是直角三角形,球心O到直角边AC的距离 即为所求.
即为所求.
 ,由A,C两点的球面距离为
,由A,C两点的球面距离为 ,可得∠AOC=60
,可得∠AOC=60 ,AC=
,AC= ,显然△ABC是直角三角形,球心O到直角边AC的距离
,显然△ABC是直角三角形,球心O到直角边AC的距离 即为所求.
即为所求.
练习册系列答案
相关题目
 ,PD^平面ABCD,PD=8,求PB
,PD^平面ABCD,PD=8,求PB 与平面ABCD所成的角的大小;
与平面ABCD所成的角的大小;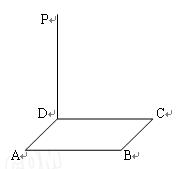
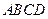 中,
中,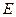 ,
,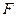 ,
,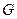 ,
,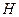 分别是
分别是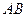 ,
,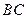 ,
, ,
,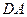 的中点.求证:四边形
的中点.求证:四边形 是平行四边形.
是平行四边形.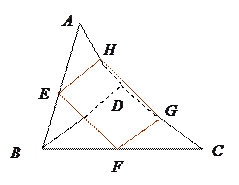
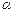 外有两条直线
外有两条直线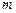 和
和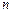 ,如果
,如果 和
和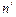 ,给出下列四个命题:
,给出下列四个命题: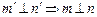

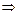
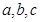 为直线,
为直线,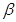 为平面,给出下列命题
为平面,给出下列命题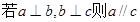 ②
②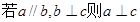
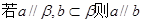 ④
④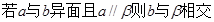
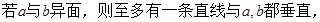 其中真命题的个数是( )
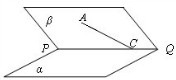
其中真命题的个数是( )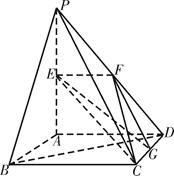 如图,平面
如图,平面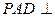 平面ABCD,
平面ABCD,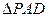 是直角三角形,
是直角三角形, ,E、F、G分别是
,E、F、G分别是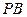 ∥面EFC;
∥面EFC;